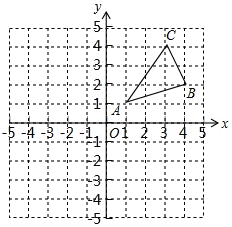��Ŀ����
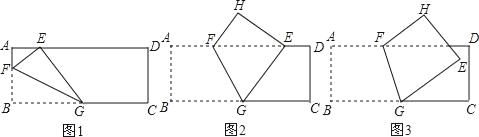
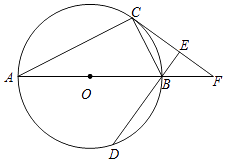
����Ŀ�����ⷢ�֣���ͼ1���ڡ�ABC�У���C=90�㣬�ֱ���AC��BCΪ���������������ACDE��������BCFG��
��1����ABC���DCF����Ĺ�ϵ���������ں�������д����ȡ�����ȡ���
��2����չ̽��������C��90�㣬��1���еĽ��ۻ�������������������ͼ2����֤����������������˵�����ɣ�
��3��������⣺��ͼ3�����ı���ABCD�У�AC��BD����AC��BD�ĺ�Ϊ10���ֱ����ı���ABCD��������Ϊ���������������ABFE��������BCHG��������CDJI��������DALK�����ã�2���Ľ��ۣ�ͼ����Ӱ���ֵ�������Ƿ������ֵ������У���������ֵ�����û�У���˵�����ɣ�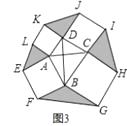
���𰸡�
��1�����
��2���⣺�������������£�
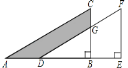
�ӳ�BC����P������A��AP��BP�ڵ�P������D��DQ��FC�ڵ�Q����ͼ��ʾ��
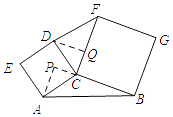
���APC=��DQC=90�㣮
���ı���ACDE��BCFG��Ϊ�����Σ�
��AC=CD��BC=CF����ACP+��PCD=90�㣬��DCQ+��PCD=90�㣬
���ACP=��DCQ��
�ڡ�APC�͡�DQC�У� 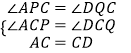 ��
��
��APC�ա�DQC��AAS����
��AP=DQ��
�֡�S��ABC= ![]() BCAP��S��DFC=
BCAP��S��DFC= ![]() FCDQ��
FCDQ��
��S��ABC=S��DFC��
��3���⣺ͼ����Ӱ���ֵ�����������ֵ���������£�
�ɣ�2���ã�S��AEL=S��ABD��S��BFG=S��ABC��S��CIH=S��CBD��S��DLK=S��DAC��
����Ӱ���ֵ����S=S��AEL+S��BFG+S��CIH+S��DLK=2S�ı���ABCD��
��AC=x����BD=10��x��
��AC��BD��
��S�ı���ABCD= ![]() AC��BD=
AC��BD= ![]() x��10��x��=��
x��10��x��=�� ![]() x2+5x=��
x2+5x=�� ![]() ��x��5��2+
��x��5��2+ ![]() ��
��
�ߩ� ![]() ��0��
��0��
��S�ı���ABCD�����ֵ�����ֵΪ ![]() ��
��
��ͼ����Ӱ���ֵ�����������ֵΪ25��
���������⣺��1����ȣ��������£�
���ı���ACDE���ı���BCFG�������Σ�
��AC=DC��BC=FC����ACD=��BCF=90�㣬
�ߡ�ACB=90�㣬
���DCF=90��=��ACB��
�ڡ�ABC���DFC�У� 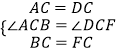 ��
��
���ABC�ա�DFC��AAS����
���ABC���DFC�������ȣ�
���Դ��ǣ���ȣ�
�����㾫����������Ҫ�����˶��κ�������ֵ�����֪ʶ�㣬��Ҫ��������Ա�����ȡֵ��Χ��ȫ��ʵ������ô�����ڶ��㴦ȡ�����ֵ������Сֵ��������x=-b/2aʱ��y��ֵ=(4ac-b2)/4a������ȷ�����⣮

 ���б�ˢ��ϵ�д�
���б�ˢ��ϵ�д�