题目内容
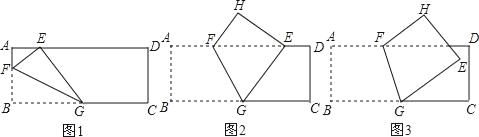
【题目】如图,长方形纸片ABCD中,AB=8,将纸片折叠,使顶点B落在边AD上的E点处,折痕的一端G点在边BC上.
(1)如图1,当折痕的另一端F在AB边上且AE=4时,求AF的长
(2)如图2,当折痕的另一端F在AD边上且BG=10时,
①求证:EF=EG.②求AF的长.
(3)如图3,当折痕的另一端F在AD边上,B点的对应点E在长方形内部,E到AD的距离为2cm,且BG=10时,求AF的长.
【答案】(1)AF=3;(2)①证明见解析;②AF=6;(3)AF=![]() .
.
【解析】
(1)根据翻折的性质可得BF=EF,然后用AF表示出EF,在Rt△AEF中,利用勾股定理列出方程求解即可;
(2)①根据翻折的性质可得∠BGF=∠EGF,再根据两直线平行,内错角相等可得∠BGF=∠EFG,从而得到∠EGF=∠EFG,再根据等角对等边证明即可;
②根据翻折的性质可得EG=BG,HE=AB,FH=AF,然后在Rt△EFH中,利用勾股定理列式计算即可得解;
(3)设EH与AD相交于点K,过点E作MN∥CD分别交AD、BC于M、N,然后求出EM、EN,在Rt△ENG中,利用勾股定理列式求出GN,再根据△GEN和△EKM相似,利用相似三角形对应边成比例列式求出EK、KM,再求出KH,然后根据△FKH和△EKM相似,利用相似三角形对应边成比例列式求解即可.
(1)∵纸片折叠后顶点B落在边AD上的E点处,
∴BF=EF,
∵AB=8,∴EF=8﹣AF,
在Rt△AEF中,AE2+AF2=EF2,
即42+AF2=(8﹣AF)2,
解得AF=3;
(2)①∵纸片折叠后顶点B落在边AD上的E点处,
∴∠BGF=∠EGF,
∵长方形纸片ABCD的边AD∥BC,
∴∠BGF=∠EFG,
∴∠EGF=∠EFG,
∴EF=EG;
②∵纸片折叠后顶点B落在边AD上的E点处,
∴EG=BG=10,HE=AB=8,FH=AF,
∴EF=EG=10,
在Rt△EFH中,FH=![]() =
=![]() =6,
=6,
∴AF=FH=6;
(3)如图3,设EH与AD相交于点K,过点E作MN∥CD分别交AD、BC于M、N,
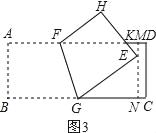
∵E到AD的距离为2cm,
∴EM=2,EN=8﹣2=6,
在Rt△ENG中,GN=![]() =
=![]() =8,
=8,
∵∠GEN+∠KEM=180°﹣∠GEH=180°﹣90°=90°,
∵∠GEN+∠NGE=180°﹣90°=90°,
∴∠KEM=∠NGE,
又∵∠ENG=∠KME=90°,
∴△GEN∽△EKM,
∴![]() ,
,
即![]() ,
,
解得EK=![]() ,KM=
,KM=![]() ,
,
∴KH=EH﹣EK=8﹣![]() =
=![]() ,
,
∵∠FKH=∠EKM,∠H=∠EMK=90°,
∴△FKH∽△EKM,
∴![]() ,
,
即 ,
,
解得FH=![]() ,
,
∴AF=FH=![]() .
.

 课课优能力培优100分系列答案
课课优能力培优100分系列答案 优百分课时互动系列答案
优百分课时互动系列答案【题目】网络商店(简称网店)是近年来迅速兴起的一种电子商务形式,小明的网店销售红枣、小米两种商品的相关信息如下表:
商品 | 红枣 | 小米 |
规格 | 1kg/袋 | 2kg/袋 |
成本(元/袋) | 40 | 38 |
售价(元/袋) | 60 | 54 |
根据上表提供的信息,解答下列问题
(1)已知今年前四个月,小明的网店销售上表中规格的红枣和小米共2000kg,获得利润2.8万元,求这前四个月小明的网店销售这种规格的红枣和小米各多少袋?
(2)根据之前的销售情况,估计今年5月到12月这后八个月,小明的网店还能销售同规格的红枣和小米共4000kg,其中,红枣的销售量不低于1200kg.假设这后八个月,销售红枣x(kg),销售红枣和小米获得的总利润为y(元),求出y与x之间的函数关系式,并求出这后八个月,小明的网店销售这种规格的红枣和小米至少获得总利润多少元?