题目内容
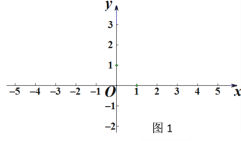
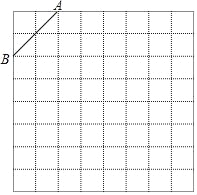
【题目】如图是规格为8×8的正方形网格,请在所给网格中按下列要求操作:
(1)在网格中建立平面直角坐标系,使A点坐标为(﹣2,4),B点坐标为(﹣4,2);
(2)在第二象限内的格点上画一点C,使点C与线段AB组成一个以AB为底的等腰三角形,且腰长是无理数,则C点坐标是 ;
(3)求△ABC中BC边上的高长.
【答案】(1)见解析;(2)(﹣1,1);(3)![]() .
.
【解析】
(1)根据A点坐标向右两个单位,再向下4个单位,可得原点,建立直角坐标系;
(2)根据勾股定理和等腰三角形的判定,可得点C的坐标,
(3)根据勾股定理,求出BC,根据图形割补法,可得面积,再根据三角形的面积公式即可得到结论.
(1)如图1:
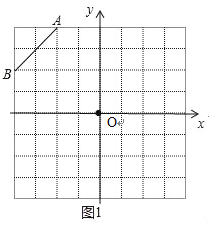
(2)如图2:
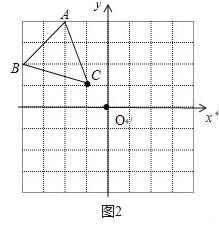
在第二象限内的格点上画一点C,使点C与线段AB组成一个以AB为底的等腰三角形,且腰长是无理数,则C点坐标是 (﹣1,1);
故答案为:(﹣1,1);
(3) 根据勾股定理得:BC=![]() ,
,
∵S△ABC=3×3﹣![]() ×1×3﹣
×1×3﹣![]() ×1×3﹣
×1×3﹣![]() ×2×2=4=
×2×2=4=![]() BC×BC边上的高 ,
BC×BC边上的高 ,
∴△ABC中BC边上的高=![]() =
=![]() .
.

练习册系列答案
相关题目