题目内容
如图，PA、PB切⊙O于点A、B，点C是⊙O上一点，且∠ACB=65°，则∠P等于（ ）
| A．65° | B．130° | C．50° | D．45° |
连接OA，OB．
PA、PB切⊙O于点A、B，则∠PAO=∠PBO=90°，
由圆周角定理知，∠AOB=2∠C=130°，
∵∠P+∠PAO+∠PBO+∠AOB=360°，
∴∠P=180°-∠AOB=50°．
故选C．
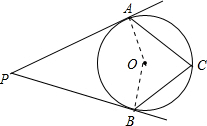
PA、PB切⊙O于点A、B，则∠PAO=∠PBO=90°，
由圆周角定理知，∠AOB=2∠C=130°，
∵∠P+∠PAO+∠PBO+∠AOB=360°，
∴∠P=180°-∠AOB=50°．
故选C．
练习册系列答案
孟建平名校考卷系列答案
相关题目
