题目内容
如图，在Rt△ABC中，∠C=90°，点O在AB上，以O为圆心，OA长为半径的圆与AC、AB分别交于D、E，且⊙O与直线BD刚好相切．
（1）试证：∠CBD=∠A；
（2）若cosA=
，BD=2
，试计算⊙O的面积．
（1）试证：∠CBD=∠A；
（2）若cosA=
2
| ||
| 5 |
| 5 |
（1）证明：连OD，如图，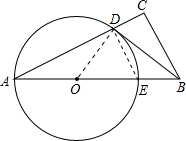
∴∠A=∠ADO，
∵直线BD与⊙O相切，
∴OD⊥BD，
∴∠ODB=90°，
∴∠ADO+∠BDC=90°，
又∵∠C=90°，
∴∠CBD+∠CDB=90°，
∴∠CBD=∠ADO，
∴∠CBD=∠A；
（2）连DE，cosA=cos∠CBD=
，
在Rt△DCB，cosA=
，BD=2
，
∴cos∠CBD=
，
∴BC=
×2
=4，
∴DC=
=2，
∵AE为直径，
∴∠ADE=90°，
在Rt△ABC中，设⊙O的半径为r，
∴cosA=
=
，
∴AD=2r•
=
r，
∴DE=
r，
∵DE∥BC，
∴DE：BC=AD：AC，即
r：4=
r：（
r+2），
∴r=
，
∴⊙O的面积=π•（
）2=
π．
∴∠A=∠ADO，
∵直线BD与⊙O相切，
∴OD⊥BD，
∴∠ODB=90°，
∴∠ADO+∠BDC=90°，
又∵∠C=90°，
∴∠CBD+∠CDB=90°，
∴∠CBD=∠ADO，
∴∠CBD=∠A；
（2）连DE，cosA=cos∠CBD=
2
| ||
| 5 |
在Rt△DCB，cosA=
2
| ||
| 5 |
| 5 |
∴cos∠CBD=
| BC |
| DB |
∴BC=
2
| ||
| 5 |
| 5 |
∴DC=
| BD2-BC2 |
∵AE为直径，
∴∠ADE=90°，
在Rt△ABC中，设⊙O的半径为r，
∴cosA=
| AD |
| AE |
2
| ||
| 5 |
∴AD=2r•
2
| ||
| 5 |
4
| ||
| 5 |
∴DE=
2
| ||
| 5 |
∵DE∥BC，
∴DE：BC=AD：AC，即
2
| ||
| 5 |
4
| ||
| 5 |
4
| ||
| 5 |
∴r=
3
| ||
| 2 |
∴⊙O的面积=π•（
3
| ||
| 2 |
| 45 |
| 4 |
练习册系列答案
相关题目
点E作EF⊥AB于点F．建立如图所示的平面直角坐标系，已知A、B两点坐标分别为A（2，0）、B（0，
作⊙O．
