ЬтФПФкШн
ЁОЬтФПЁПТЎбєДКЗчЬхг§дЫЖЏЦЗЩЬЕъДгГЇМвЙКНјМзЃЌввСНжжTаєЙВ400МўЃЌЦфУПМўЕФЪлМлгыНјЛѕСПmЃЈМўЃЉжЎМфЕФЙиЯЕМАГЩБОШчЯТБэЫљЪОЃК
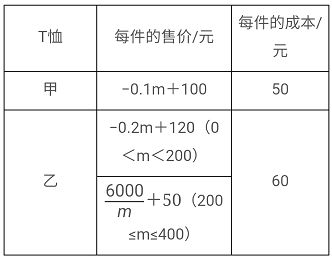
ЃЈ1ЃЉЕБМзжжTаєНјЛѕ250МўЪБЃЌЧѓСНжжTаєШЋВПЪлЭъЕФРћШѓЪЧЖрЩйдЊ.
ЃЈ2ЃЉШєЫљгаЕФTаєЖМФмЪлЭъЃЌЧѓИУЕъЛёЕУЕФзмРћШѓyЃЈдЊЃЉгыввжжTаєЕФНјЛѕСПxЃЈМўЃЉжЎМфЕФКЏЪ§ЙиЯЕЪНЃЛ
ЃЈ3ЃЉдкЃЈ2ЃЉЕФЬѕМўЯТвбжЊСНжжTаєНјЛѕСПЖМВЛЕЭгк100МўЃЌЧвЫљНјЕФTаєШЋВПЪлЭъЃЌИУЩЬЕъШчКЮАВХХНјЛѕВХФмЛёЕУЕФРћШѓзюДѓЃП
ЁОД№АИЁПЃЈ1ЃЉ10750ЃЛЃЈ2ЃЉЕБ![]() ЪБЃЌ
ЪБЃЌ![]() ЃЛЕБ
ЃЛЕБ![]() ЪБЃЌ
ЪБЃЌ![]() ЃЛЃЈ3ЃЉЕБЙКНјМзжж
ЃЛЃЈ3ЃЉЕБЙКНјМзжж![]() ає250МўЁЂввжж
ає250МўЁЂввжж![]() ає150МўЪБЃЌВХФмЪЙЛёЕУЕФРћШѓзюДѓ
ає150МўЪБЃЌВХФмЪЙЛёЕУЕФРћШѓзюДѓ
ЁОНтЮіЁП
ЃЈ1ЃЉИљОнЯњЪлРћШѓЃНЕЅМўРћШѓЁСЯњЪлСПЃЌНЋМзЁЂввСНжжTаєЕФРћШѓЯрМгПЩЕУД№АИЃЛ
ЃЈ2ЃЉЗж0ЃМxЃМ200КЭ200ЁмxЁм400СНжжЧщПіЃЌИљОнзмРћШѓЃНМзжжTаєЕФРћШѓЃЋввжжTаєЕФРћШѓКЭTаєРћШѓЃНЕЅМўРћШѓЁСЯњЪлСПСаГіКЏЪ§НтЮіЪНЃЛ
ЃЈ3ЃЉЗж100ЁмxЃМ200КЭ200ЁмxЁм300СНжжЧщПіЃЌНЋЖдгІНтЮіЪНХфЗНГЩЖЅЕуЪНЃЌдйРћгУЖўДЮКЏЪ§ЕФаджЪЧѓНтПЩЕУЃЎ
НтЃКЃЈ1ЃЉЕБМзжж![]() аєНјЛѕ250МўЪБЃЌввжжTаєНјЛѕ150МўЃЌ
аєНјЛѕ250МўЪБЃЌввжжTаєНјЛѕ150МўЃЌ
ИљОнЬтвтжЊСНжж![]() аєШЋВПЪлЭъЕФРћШѓЪЧЃК
аєШЋВПЪлЭъЕФРћШѓЪЧЃК
![]() ЃЈдЊЃЉЃЛ
ЃЈдЊЃЉЃЛ
ЃЈ2ЃЉЕБ![]() ЪБЃЌ
ЪБЃЌ
![]() ЃЛ
ЃЛ
ЕБ![]() ЪБЃЌ
ЪБЃЌ
![]() ЃЛ
ЃЛ
ЃЈ3ЃЉгЩЬтвтЕУЃК![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ
НтЕУЃК![]() ЃЌ
ЃЌ
Шє![]() ЃЌдђ
ЃЌдђ![]() ЃЌ
ЃЌ
ЕБ![]() ЪБЃЌ
ЪБЃЌ![]() ЕФзюДѓжЕЮЊ10750ЃЛ
ЕФзюДѓжЕЮЊ10750ЃЛ
Шє![]() ЪБЃЌ
ЪБЃЌ![]() ЃЌ
ЃЌ
Ёп![]() ЪБЃЌ
ЪБЃЌ![]() Ыц
Ыц![]() ЕФдіДѓЖјМѕаЁЃЌ
ЕФдіДѓЖјМѕаЁЃЌ
ЁрЕБ![]() ЪБЃЌ
ЪБЃЌ![]() ШЁЕУзюДѓжЕЃЌзюДѓжЕЮЊ10000дЊЃЛ
ШЁЕУзюДѓжЕЃЌзюДѓжЕЮЊ10000дЊЃЛ
злЩЯЃЌЕБЙКНјМзжж![]() ає250МўЁЂввжж
ає250МўЁЂввжж![]() ає150МўЪБЃЌВХФмЪЙЛёЕУЕФРћШѓзюДѓЃЎ
ає150МўЪБЃЌВХФмЪЙЛёЕУЕФРћШѓзюДѓЃЎ

 дФЖСПьГЕЯЕСаД№АИ
дФЖСПьГЕЯЕСаД№АИЁОЬтФПЁПЕкЖўЪЎЫФНьЖЌМОАТСжЦЅПЫдЫЖЏЛсНЋгы2022Фъ2дТ20ШедкББОЉОйааЃЌББОЉНЋГЩЮЊРњЪЗЩЯЕквЛзљОйАьЙ§ЯФАТЛсгжОйАьЙ§ЖЌАТЛсЕФГЧЪаЃЌЖЋБІЧјОйАьСЫвЛДЮЖЌАТЛсжЊЪЖЭјЩЯД№ЬтОКШќЃЌМзЁЂввСНаЃИїга400УћбЇЩњВЮМгЛюЖЏЃЌЮЊСЫНтетСНЫљбЇаЃЕФГЩМЈЧщПіЃЌНјааСЫГщбљЕїВщЃЌЙ§ГЬШчЯТЃЌЧыВЙГфЭъећЃЎ
ЃЈЪеМЏЪ§ОнЃЉ
ДгМзЁЂввСНаЃИїЫцЛњГщШЁ20УћбЇЩњЃЌдкетДЮОКШќжаЫќУЧЕФГЩМЈШчЯТЃК
Мз | 30 | 60 | 60 | 70 | 60 | 80 | 30 | 90 | 100 | 60 |
60 | 100 | 80 | 60 | 70 | 60 | 60 | 90 | 60 | 60 | |
вв | 80 | 90 | 40 | 60 | 80 | 80 | 90 | 40 | 80 | 50 |
80 | 70 | 70 | 70 | 70 | 60 | 80 | 50 | 80 | 80 |
ЃЈећРэЁЂУшЪіЪ§ОнЃЉАДШчЯТЗжЪ§ЖЮећРэЁЂУшЪіетСНзщбљБОЪ§ОнЃК
ЃЈЫЕУїЃКгХауГЩМЈЮЊ80ЃМxЁм100ЃЌСМКУГЩМЈЮЊ50ЃМxЁм80ЃЌКЯИёГЩМЈЮЊ30ЁмxЁм50ЃЎЃЉ
бЇаЃ | ЦНОљЗж | жаЮЛЪ§ | жкЪ§ |
Мз | 67 | 60 | 60 |
вв | 70 | 75 | a |
30ЁмxЁм50 | 50ЃМxЁм80 | 80ЃМxЁм100 | |
Мз | 2 | 14 | 4 |
вв | 4 | 14 | 2 |
ЃЈЗжЮіЪ§ОнЃЉСНзщбљБОЪ§ОнЕФЦНОљЗжЁЂжаЮЛЪ§ЁЂжкЪ§ШчгвБэЫљЪОЃКЦфжаa=ЁЁЁЁЃЎ
ЃЈЕУГіНсТлЃЉ
ЃЈ1ЃЉаЁЮАЭЌбЇЫЕЃКЁАетДЮОКШќЮвЕУСЫ70ЗжЃЌдкЮвУЧбЇаЃХХУћЪєжагЮТдЦЋЩЯЃЁЁБгЩБэжаЪ§ОнПЩжЊаЁУїЪЧЁЁЁЁаЃЕФбЇЩњЃЛЃЈЬюЁАМзЁБЛђЁАввЁБЃЉ
ЃЈ2ЃЉРЯЪІДгвваЃЫцЛњГщШЁвЛУћбЇЩњЕФОКШќГЩМЈЃЌЪдЙРМЦетУћбЇЩњЕФОКШќГЩМЈЮЊгХауЕФИХТЪЮЊЁЁЁЁЃЛ
ЃЈ3ЃЉИљОнвдЩЯЪ§ОнЭЦЖЯвЛЫљФуШЯЮЊОКШќГЩМЈНЯКУЕФбЇаЃЃЌВЂЫЕУїРэгЩЃЎЃЈжСЩйДгСНИіВЛЭЌЕФНЧЖШЫЕУїЭЦЖЯЕФКЯРэадЃЉ
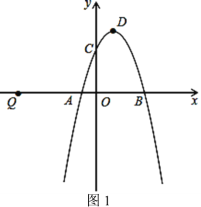
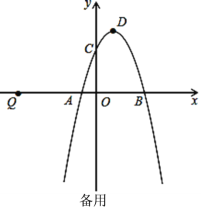
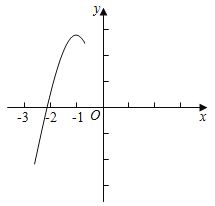
ЁОЬтФПЁПвбжЊЖўДЮКЏЪ§ЕФНтЮіЪНЪЧyЃНx2Љ2xЉ3ЃЎ
ЃЈ1ЃЉгыyжсЕФНЛЕузјБъЪЧЁЁ ЁЁЃЌЖЅЕузјБъЪЧЁЁ ЁЁЃЎ
ЃЈ2ЃЉдкзјБъЯЕжаРћгУУшЕуЗЈЛГіДЫХзЮяЯпЃЛ
x | Ё | Ё | |||||
y | Ё | Ё |
ЃЈ3ЃЉНсКЯЭМЯѓЛиД№ЃКЕБЉ2ЃМxЃМ2ЪБЃЌКЏЪ§жЕyЕФШЁжЕЗЖЮЇЪЧЁЁ ЁЁЃЎ