题目内容
【题目】如图，
是等腰
内一点，
，且
，
，
．将
绕点
按逆时针方向旋转后，得到
．
直接写出旋转的最小角度；
求
的度数．
【答案】（1）90°；（2）135°；
【解析】
（1）由等腰直角三角形的性质得CA=CB，∠ACB=90°，再根据旋转的性质得∠ACB等于旋转角，于是可判断旋转的最小角度为90°；
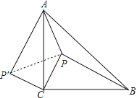
（2）连结PP′，如图，根据旋转的性质得∠P′CP=∠ACB=90°，CP′=CP=
，P′A=PB=10，则可判断△CPP′为等腰直角三角形，得到PP′=
CP=6，∠CPP′=45°，然后利用勾股定理的逆定理判断△APP′为直角三角形，∠APP′=90°，于是利用∠APC=∠APP′+∠CPP′计算即可．
∵
为等腰直角三角形，
∴
，
，
∵
绕点
按逆时针方向旋转后，得到
，
∴
等于旋转角，
∴旋转的最小角度为
；
连结
，如图，
∵绕点按逆时针方向旋转后，得到，
∴
，
，
，
∴
为等腰直角三角形，
∴
，
，
在
中，∵
，
，
，
∴
，
∴为直角三角形，
，
∴
．
练习册系列答案
阅读快车系列答案
相关题目
