��Ŀ����
����Ŀ�����ǰ�����������������ABC��Ϊ���ƽ�����������
����ABC�ǵ��������Σ����������ε�ij�����ϴ��ڲ��붥���غϵĵ�P��ʹ��P��P���ڱߵĶԽǶ������߰���ABC�ֳ�������ȫ���ĵ���������.
��1����ABC�У�AB=AC����A:��C=1:2,��֤��ABC�����ƽ���������,��ʱ��A�Ķ���Ϊ_________.
��2����ABC�У�AB=AC, ��AΪ�۽�.����ABCΪ���ƽ��������������A�Ķ���Ϊ________.
���𰸡�![]()
![]()
��������
��1�����ݵ��������ε����ʼ��������ڽǺ���⼴�ɣ�
��2������ͼ�Σ����ݵ������������ʡ���Ƕ������������ڽǺͼ��������.
�⣺��1���ߡ�A����C=1��2,
������A=x������C=2x��
��AB=AC��
���B=��C=2x��
�ߡ�A+��B+��C=180����
��x+2x+2x=180����
��x=36��������A=36����
��2����ABC��ͼ��ʾ��
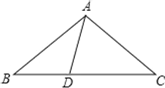
�ߡ�ABCΪ���ƽ�����������
��AB=AC��AD=BD��AC=CD��
���B=��C=��BAD����CAD=��CDA��
�ߡ�CDA=��B+��BAD=2��B��
���BAC=��BAD+��CAD=3��B��
�ߡ�BAC+��B+��C=180����
��5��B=180����
���B=36����
���BAC=108����
�ʴ�Ϊ��36�㣻 108��.