题目内容
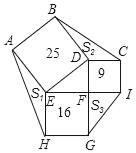
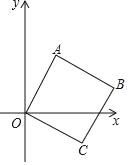
【题目】如图,在正方形![]() 中,
中,![]() .点
.点![]() 为
为![]() 边上一点(不与点
边上一点(不与点![]() 重合),点
重合),点![]() 为
为![]() 边上一点,线段
边上一点,线段![]() 、
、![]() 相交于点
相交于点![]() ,其中
,其中![]() .
.

![]() 求证:
求证:![]() ;
;
![]() 若
若![]() ,求
,求![]() 的长及四边形
的长及四边形![]() 的面积;
的面积;
![]() 连接
连接![]() ,若
,若![]() 是以
是以![]() 为腰的等腰三角形,求
为腰的等腰三角形,求![]() 的长.
的长.
【答案】(1)详见解析;(2)6;(3)![]() .
.
【解析】
(1)只要证明△ABE≌△BCF,即可推出∠BAE=∠CBF,由∠BAE+∠AEB=90°,推出∠CBF+∠AEB=90°,推出∠BOE=90°;
(2)设OB=x,则OA=x+1,在Rt△AOB中,由AB2=OA2+OB2,可得x2+(x+1)2=52,推出x=3或-4(舍弃),推出OA=4,OB=3,根据S四边形OECF=S△AOB计算即可;
(3)作DH⊥OA于H.易证△ADH≌△BAO,推出AH=OB,由△ADO是AD为腰的等腰三角形,OA<AB=AD,推出只有AD=OD,推出AH=OH=OB,设AH=OH=OB=a,可得(2a)2+a2=52,推出a=![]() ,推出OA=2
,推出OA=2![]() ,由cos∠BAE=
,由cos∠BAE=![]() ,列出方程即可解决问题;
,列出方程即可解决问题;
![]() 证明:∵四边形
证明:∵四边形![]() 是正方形,
是正方形,
∴![]() ,
,![]() ,
,
在![]() 和
和![]() 中,
中,
![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() .
.
![]() 设
设![]() ,则
,则![]() ,
,
在![]() 中,∵
中,∵![]() ,
,
∴![]() ,
,
∴![]() 或
或![]() (舍弃),
(舍弃),

∴![]() ,
,![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() .
.
![]() 作
作![]() 于
于![]() .易证
.易证![]() ,
,
∴![]() ,
,
∵![]() 是
是![]() 为腰的等腰三角形,
为腰的等腰三角形,![]() ,
,
∴只有![]() ,
,
∴![]() ,设
,设![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() .
.

 名校课堂系列答案
名校课堂系列答案【题目】元旦期间,为了满足颍上县百姓的消费需要,某大型商场计划用170000元购进一批家电,这批家里的进价和售价如表:
类别 | 彩电 | 冰箱 | 洗衣机 |
进价(元/台) | 2000 | 1600 | 1000 |
售价(元/台) | 2300 | 1800 | 1100 |
若在现有资金允许的范围内,购买表中三类家电共100台,其中彩电台数是冰箱台数的2倍,设该商场购买冰箱x台.
(1)用含x的代数式表示洗衣机的台数.
(2)商场至多可以购买冰箱多少台?
(3)购买冰箱多少台时,能使商场销售完这批家电后获得的利润最大?最大利润为多少元?