题目内容
已知，在平面直角坐标系中，反比例函数y=
（k≠0）的图象与一次函数y=x+b的图象交于A（-1，b-1）、B（-5，b-5）两点．
（1）求反比例函数与一次函数的解析式；
（2）设抛物线y=-x2+b′x+c（c＞0）的顶点P在直线AB上，且PA：PB=1：3，求抛物线的解析式；
（3）把以上函数图象同步向右平移，使直线AB与两坐标轴所围成的三角形的面积等于2，求平移后的抛物线的解析式．
| k |
| x |
（1）求反比例函数与一次函数的解析式；
（2）设抛物线y=-x2+b′x+c（c＞0）的顶点P在直线AB上，且PA：PB=1：3，求抛物线的解析式；
（3）把以上函数图象同步向右平移，使直线AB与两坐标轴所围成的三角形的面积等于2，求平移后的抛物线的解析式．
（1）把A（-1，b-1）、B（-5，b-5）两点代入y=
，得：
，
解得：
，
∴正比例函数解析式为：y=x+6，
反比例函数反比例函数解析式为：y=-
；
（2）∵直线AB为y=x+6，且A（-1，5），B（-5，1），
过点A，B分别作y轴、x轴的平行线，它们相交于点C（-1，1），
则AC=BC=4，
①P点在线段AB上时，作PE∥BC，交AC于E，作PD∥AC交BC于D，
则
=
，
=
，
∵
=
，
∴
=
，
=
，
∴PE=1，PD=3，
∴P（-2，4），
∴抛物线的解析式为：y=-（x-1） 2+4，
即y=-x 2-4x，
此时，c=0，不符合题意，舍去；
②当P点在线段BA的延长线上时，同理可得：P（1，7）
∴抛物线的解析式为：y=-（x-1） 2+7，
即y=-x 2+2x+6，
此时，c=6＞0，符合题意，
∴由①、②可知，抛物线的解析式为：y=-x 2+2x+6；
（3）设平移后的直线解析式为：y=x+t，
它交x轴于点（-t，0），交y轴于点（0，t），
∴S△=
×|-t|×|t|=2，
∴t=±2，
∴平移后的直线解析式为：y=x+2或y=x-2，
即图象向右平移了4个单位或8个单位，
此时的抛物线解析式为：y=-（x-1-4）2+7或y=-（x-1-8）2+7，
即y=-x 2+10x-18或y=-x 2+18x-74．
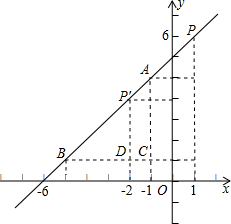
| k |
| x |
|
解得：
|
∴正比例函数解析式为：y=x+6，
反比例函数反比例函数解析式为：y=-
| 5 |
| x |
（2）∵直线AB为y=x+6，且A（-1，5），B（-5，1），
过点A，B分别作y轴、x轴的平行线，它们相交于点C（-1，1），
则AC=BC=4，
①P点在线段AB上时，作PE∥BC，交AC于E，作PD∥AC交BC于D，
则
| PE |
| BC |
| PA |
| AB |
| PD |
| AC |
| PB |
| AB |
∵
| PA |
| PB |
| 1 |
| 3 |
∴
| PA |
| AB |
| 1 |
| 4 |
| PB |
| AB |
| 3 |
| 4 |
∴PE=1，PD=3，
∴P（-2，4），
∴抛物线的解析式为：y=-（x-1） 2+4，
即y=-x 2-4x，
此时，c=0，不符合题意，舍去；
②当P点在线段BA的延长线上时，同理可得：P（1，7）
∴抛物线的解析式为：y=-（x-1） 2+7，
即y=-x 2+2x+6，
此时，c=6＞0，符合题意，
∴由①、②可知，抛物线的解析式为：y=-x 2+2x+6；
（3）设平移后的直线解析式为：y=x+t，
它交x轴于点（-t，0），交y轴于点（0，t），
∴S△=
| 1 |
| 2 |
∴t=±2，
∴平移后的直线解析式为：y=x+2或y=x-2，
即图象向右平移了4个单位或8个单位，
此时的抛物线解析式为：y=-（x-1-4）2+7或y=-（x-1-8）2+7，
即y=-x 2+10x-18或y=-x 2+18x-74．
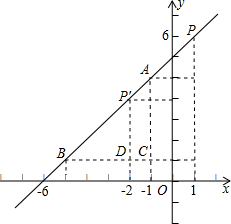
练习册系列答案
新编小学单元自测题系列答案
字词句段篇系列答案
相关题目
标为4．
