��Ŀ����
����Ŀ����ƽ��ֱ������ϵ�У����Dz����Ѻ���������������ȵĵ��Ϊ��֮�㣬���磬�㣨1��1�������� 2���� 2������![]() ��
��![]() ��������������֮�㣬��Ȼ��֮������������
��������������֮�㣬��Ȼ��֮������������
��1������ P��2��b���Ƿ���������![]() (n Ϊ������n �� 0) ��ͼ���ϵ���֮�㣬�������������������ʽ��
(n Ϊ������n �� 0) ��ͼ���ϵ���֮�㣬�������������������ʽ��
��2����O �İ뾶��![]() ��
��
�������O�ϵ�������֮������ꣻ
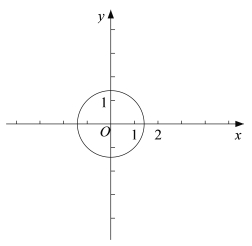
����֪�� M��m��3������ Q �ǣ�1���з���������![]() ͼ�������ڵ� P ����֮�㣬����Q ��ֱ�� l �� y �ύ�ڵ� A����OAQ��45�������ڡ� O �ϴ���һ�� N��ʹ��ֱ�� MN �� l�� MN �� l����� m ��ȡֵ��Χ��
ͼ�������ڵ� P ����֮�㣬����Q ��ֱ�� l �� y �ύ�ڵ� A����OAQ��45�������ڡ� O �ϴ���һ�� N��ʹ��ֱ�� MN �� l�� MN �� l����� m ��ȡֵ��Χ��
���𰸡���1��![]() ����2������O��������֮�������ǣ�1��1����-1��-1������m��ȡֵ��ΧΪ-5��m��-1��1��m��5��
����2������O��������֮�������ǣ�1��1����-1��-1������m��ȡֵ��ΧΪ-5��m��-1��1��m��5��
��������
��1������֮��Ķ�������P�����꣬�����ô���ϵ��������÷�������������ʽ����2�������O�ϵ���֮������Ϊ��a��a������Բ�İ뾶�����ݹ��ɶ����ɵõ�����a�ķ��̣������a��ֵ����ɵ���֮������ꣻ�ڷ���������������ۣ���MNΪy=-x+bʱ��m=b-3����ֱ��MNƽ�������O����ʱ�����е��ڵ�������ʱ��bȡ����Сֵ����ֱ��MNƽ�������O����ʱ�����е��ڵ�һ����ʱ��bȡ�����ֵ���ݴ˿ɵ�m��ȡֵ��ΧΪ-5��m��-1����ֱ��MNΪy=x+bʱ��ͬ���ɵã�m��ȡֵ��ΧΪ1��m��5��
��1�� ��P��2��b������֮������b=2
��P��2��2��
��P��2��2�� ����![]() �е�n=4
�е�n=4
�෴������������ʽ��![]()
��2��������O����֮�������ǣ�![]() ��
��![]() ����
����![]() ��
��![]()
![]() =1��
=1��![]() =-1
=-1
����O��������֮�������ǣ�1��1����-1��-1��
������1��֪�����ڵ�P����֮��Q������Ϊ��-2��-2��
����֪MN��l��MN��l

��ֱ��MNΪy=-x+b��y=x+b
��MNΪy=-x+bʱ��m=b-3
��ͼ��֪����ֱ��MNƽ��������O����ʱ��
���е��ڵ�������ʱ��bȡ����Сֵ��
��ʱMN ��Ϊ![]() ��
��
���� ![]() Ϊ�е㣬
Ϊ�е㣬![]() Ϊֱ����y��Ľ���
Ϊֱ����y��Ľ���
�ߡ�O![]()
![]() Ϊ��Ҫֱ�������Σ�
Ϊ��Ҫֱ�������Σ�
��O![]() =
=![]() ��O
��O![]() =2
=2
��b����Сֵ��-2��
��m����Сֵ��-5
��ֱ��MNƽ��������O����ʱ�����е��ڵڶ�����ʱ��
bȡ�����ֵ����ʱMN ��Ϊ![]() ��
��
���� ![]() Ϊ�е㣬
Ϊ�е㣬![]() Ϊֱ��
Ϊֱ��![]() ��y��Ľ��㡣
��y��Ľ��㡣
ͬ���ɵã�b�����ֵΪ2��m�����ֵΪ-1��
��m��ȡֵ��ΧΪ-5��m��-1��
��ֱ��MNΪy=x+bʱ��
ͬ���ɵã�m��ȡֵ��ΧΪ1��m��5��
����������m��ȡֵ��ΧΪ-5��m��-1��1��m��5��