题目内容
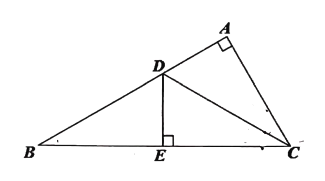
【题目】定义:如图1,在△ABC和△ADE中,AB=AC=AD=AE,当∠BAC+∠DAE=180° 时,我们称△ABC与△DAE互为“顶补等腰三角形”,△ABC的边BC上的高线AM叫做△ADE的“顶心距”,点A叫做“旋补中心”.
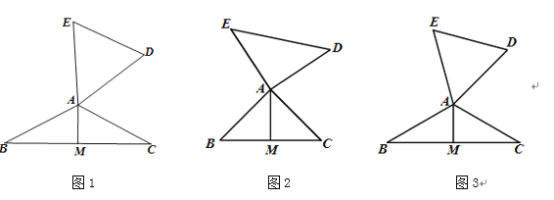
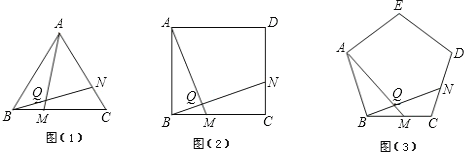
(1)特例感知:在图2,图3中,△ABC与△DAE互为“顶补等腰三角形”,AM是“顶心距”。
①如图2,当∠BAC=90°时,AM与DE之间的数量关系为AM= DE;
②如图3,当∠BAC=120°,ED=6时,AM的长为 。
(2)猜想论证:
在图1中,当∠BAC为任意角时,猜想AM与DE之间的数量关系,并给予证明。
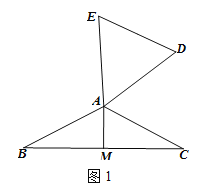
(3)拓展应用
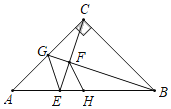
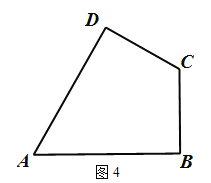
如图4,在四边形ABCD中,AD=AB,CD=BC,∠B=90°,∠A=60°,CA=![]() ,在四边ABCD的内部找到点P,使得△PAD与△PBC互为“顶补等腰三角形”。并回答下列问题。
,在四边ABCD的内部找到点P,使得△PAD与△PBC互为“顶补等腰三角形”。并回答下列问题。
①请在图中标出点P的位置,并描述出该点的位置为 ;
②直接写出△PBC的“顶心距”的长为 。
【答案】(1)①![]() ;②3(2)AM=
;②3(2)AM=![]() DE(3)
DE(3)![]()
【解析】
(1)①根据全等三角形的判定与性质推出△ABC与△DAE全等,再根据等腰直角三角形斜边上的高等于斜边的一半即可得出答案;②根据题意推出△ADE为等边三角形,推出AB的长度为6,即可得出AM (2) 过点A作AN⊥ED于N,证出∠DAN=![]() ∠DAE,ND =
∠DAE,ND =![]() DE和∠CAM=
DE和∠CAM=![]() ∠CAB,再证∠DAN+∠CAM=90°,∠DAN=∠C,推出
∠CAB,再证∠DAN+∠CAM=90°,∠DAN=∠C,推出
△AND≌△AMC,即可得出答案.
(1)①![]() ;②3
;②3
(2)猜想:结论AM=![]() DE.
DE.
证明:过点A作AN⊥ED于N
∵AE=AD,AN⊥ED
∴∠DAN=![]() ∠DAE,ND =
∠DAE,ND =![]() DE
DE
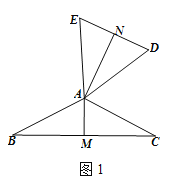
同理可得:∠CAM=![]() ∠CAB,
∠CAB,
∵∠DAE+∠CAB=180°,
∴∠DAN+∠CAM=90°,
∵∠CAM+∠C=90°
∴∠DAN=∠C,
∵AM⊥BC∴∠AMC=∠AND=90°
在△AND与△AMC中,
![]()
∴△AND≌△AMC,
∴ND=AM
∴AM=![]() DE.
DE.
(3)①图略;线段AC的中点或(线段AD的垂直平分线与线段AC的交点)或(线段BC的垂直平分线与线段AC的交点)等方法正确均可以给分;
②
PE为所求,由题意知,BC=![]() ,AB=
,AB=![]() ,
,
所以PE=![]() AB=
AB=![]()

 阅读快车系列答案
阅读快车系列答案