��Ŀ����
�ڡ�ABC�У���C=90�㣬AC=BC=2����һ�����ǰ��ֱ�Ƕ������б��AB���е�P�����������ǰ��Ƶ�P��ת�����ǰ����ֱ�DZ߷ֱ�����AC��CB���D����E��ͼ�٣��ڣ�������ת�õ�������ͼ�Ρ�

��1���۲��߶�PD��PE֮����������Ĵ�С��ϵ������ͼ��Ϊ��������˵����
��2����PBE�Ƿɵ��������Σ����ܣ�ָ�����е�������������PBEΪ����������ʱCE�ij���ֱ��д�����������������˵�����ɡ�

��1���۲��߶�PD��PE֮����������Ĵ�С��ϵ������ͼ��Ϊ��������˵����
��2����PBE�Ƿɵ��������Σ����ܣ�ָ�����е�������������PBEΪ����������ʱCE�ij���ֱ��д�����������������˵�����ɡ�
�⣺1��PD=PE����ͼ��Ϊ������PC
�ߡ�ABC�ǵ���ֱ�������Σ�PΪб��AB���е㣬
��PC=PB��CP��AB����DCP=��B=45�㣬 ���������������������������� 1��
�֡ߡ�DPC+��CPE=90�㣬��CPE+��EPB=90��
���DPC=��EPB������������������1��
���DPC�ա�EPB��AAS��������������������1��
��PD=PE��������������������������1��
2���ܣ��ٵ�EP=EBʱ��CE= ��������������������������1��
��������������������������1��
�ڵ�EP=PBʱ����E ��BC�ϣ����E��C�غϣ�CE=0������1��
�۵�BE=BPʱ������E��BC�ϣ���CE=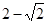 ����������1��
����������1��
����E��CB���ӳ����ϣ���CE= ������1��
������1��
�ߡ�ABC�ǵ���ֱ�������Σ�PΪб��AB���е㣬
��PC=PB��CP��AB����DCP=��B=45�㣬 ���������������������������� 1��
�֡ߡ�DPC+��CPE=90�㣬��CPE+��EPB=90��
���DPC=��EPB������������������1��
���DPC�ա�EPB��AAS��������������������1��
��PD=PE��������������������������1��
2���ܣ��ٵ�EP=EBʱ��CE=
 ��������������������������1��
��������������������������1���ڵ�EP=PBʱ����E ��BC�ϣ����E��C�غϣ�CE=0������1��
�۵�BE=BPʱ������E��BC�ϣ���CE=
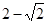 ����������1��
����������1������E��CB���ӳ����ϣ���CE=
 ������1��
������1����1������PC��ͨ��֤����PCD�ա�PBE���ó�PD=PE��
��2����Ϊ��C���E�غϡ�CE=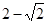 ��CE=1��E��CB���ӳ����������������˵����
��CE=1��E��CB���ӳ����������������˵����
��2����Ϊ��C���E�غϡ�CE=
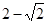 ��CE=1��E��CB���ӳ����������������˵����
��CE=1��E��CB���ӳ����������������˵����
��ϰ��ϵ�д�
 �·Ƿ��̸����100��ϵ�д�
�·Ƿ��̸����100��ϵ�д�
�����Ŀ




 �������������У�ÿ��С�����εı߳���Ϊ1���������������а�����Ҫ��ͼ�Σ�
�������������У�ÿ��С�����εı߳���Ϊ1���������������а�����Ҫ��ͼ�Σ� ��
��