题目内容
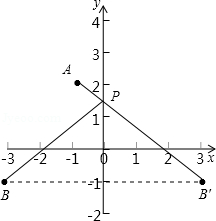
已知A（﹣1，2）和B（﹣3，﹣1）．试在y轴上确定一点P，使其到A、B的距离和最小，求P点的坐标．
解：如图所示，出B点关于y轴的对称点B′，连接AB′交y轴于点P，
设过A、B′两点的一次函数解析式为y=kx+b（k≠0），
则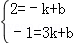
，解得k=﹣
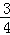，b=
，
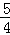故此一次函数的解析式为：y=﹣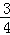x+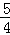，当x=0时，y=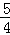，故P点坐标
为（0，）．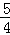
故答案为：P（0，）．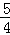
设过A、B′两点的一次函数解析式为y=kx+b（k≠0），
则
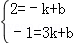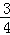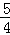，解得k=﹣，b=，故此一次函数的解析式为：y=﹣
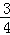x+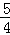，当x=0时，y=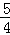，故P点坐标为（0，
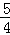）．故答案为：P（0，
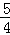）．作出B点关于y轴的对称点B′，连接AB′交y轴于点P，由两点之间线段最短可知，点P即为所求点，用待定系数法求出过AB′的一次函数解析式，再求出此函数与y轴的交点即可．
练习册系列答案
互动课堂系列答案
激活思维智能训练课时导学练系列答案
相关题目
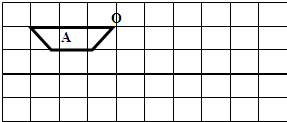
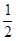
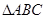，请你画出格点
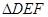，使