题目内容
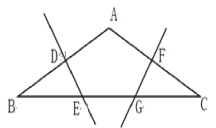
【题目】如图,AB=AC,∠A=120,BC=6cm,ED、FG分别是AB,AC的垂直平分线,求BE的长.
【答案】BE=2cm.
【解析】
连接AE、AG,根据等腰三角形的性质可得:∠B=∠C=30°,然后根据垂直平分线的性质可得:BE=AE,AG=CG,从而得出:∠B=∠BAE=30°,∠C=∠CAG=30°,然后根据三角形外角的性质可得:∠AEG=∠AGE=60°,再根据等边三角形的判定可得:△AEG是等边三角形,从而得出:AE=EG=AG,即可求出BE= EG= CG =2cm.
解:连接AE、AG,

∵AB=AC,∠BAC=120°,
∴∠B=∠C=30°,
∵DE、FG分别为线段AB、AC的垂直平分线,
∴BE=AE,AG=CG,
∴∠B=∠BAE=30°,∠C=∠CAG=30°,
∵∠AEG与∠AGE分别是△AEB与△AGC的外角,
∴∠AEG=∠B+∠BAE=30°+30°=60°,∠AGE=∠C+∠CAG=30°+30°=60°,
∴△AEG是等边三角形,
∴AE=EG=AG,
∵BE=AE,AG=CG,BC=6cm,
∴BE= EG= CG =2cm.

练习册系列答案
相关题目