题目内容
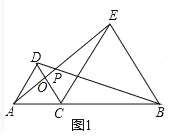
【题目】如图1,点C在线段AB上,(点C不与A、B重合),分别以AC、BC为边在AB同侧作等边三角形ACD和等边三角形BCE,连接AE、BD交于点P.
(观察猜想)
①AE与BD的数量关系是 ;
②∠APD的度数为 .
(数学思考)
如图2,当点C在线段AB外时,(1)中的结论①、②是否仍然成立?若成立,请给予证明;若不成立,请你写出正确结论再给予证明;
(拓展应用)
如图3,点E为四边形ABCD内一点,且满足∠AED=∠BEC=90°,AE=DE,BE=CE,对角线AC、BD交于点P,AC=10,则四边形ABCD的面积为 .

【答案】【观察猜想】:①AE=BD.②∠APD=60°.理由见解析;【数学思考】:结论仍然成立,证明见解析;【拓展应用】:50.
【解析】
观察猜想:证明△ACE≌△DCB(SAS),可得AE=BD,∠CAO=∠ODP,由∠AOC=∠DOP,推出∠DPO=∠ACO=60°;
数学思考:结论成立,证明方法类似;
拓展应用:证明AC⊥BD,可得S四边形ABCD=![]() ACDP+
ACDP+![]() ACPB=
ACPB=![]() AC(DP+PB)=
AC(DP+PB)=![]() ACBD.
ACBD.
观察猜想:结论:AE=BD.∠APD=60°.
理由:设AE交CD于点O.
∵△ADC,△ECB都是等边三角形,
∴CA=CD,∠ACD=∠ECB=60°,CE=CB,
∴∠ACE=∠DCB,
∴△ACE≌△DCB(SAS),
∴AE=BD,∠CAO=∠ODP,
∵∠AOC=∠DOP,
∴∠DPO=∠ACO=60°,
即∠APD=60°.
故答案为AE=BD,60°.
数学思考:结论仍然成立.
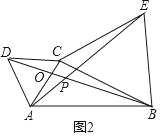
理由:设AC交BD于点O.
∵△ADC,△ECB都是等边三角形,
∴CA=CD,∠ACD=∠ECB=60°,CE=CB,
∴∠ACE=∠DCB
∴△ACE≌△DCB(SAS),
∴AE=BD,∠PAO=∠ODC,
∵∠AOP=∠DOC,
∴∠APO=∠DCO=60°,
即∠APD=60°.
拓展应用:
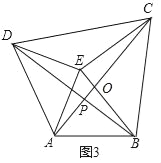
设AC交BE于点O.
∵△ADE,△ECB都是等腰直角三角形,
∴ED=EA,∠AED=∠BEC=90°,CE=EB,
∴∠AEC=∠DEB
∴△AEC≌△DEB(SAS),
∴AC=BD=10,∠PBO=∠OCE,
∵∠BOP=∠EOC,
∴∠BPO=∠CEO=90°,
∴AC⊥BD,
∴S四边形ABCD=![]() ACDP+
ACDP+![]() ACPB=
ACPB=![]() AC(DP+PB)=
AC(DP+PB)=![]() ACBD=50.
ACBD=50.
故答案为:50.

 黄冈冠军课课练系列答案
黄冈冠军课课练系列答案【题目】某童装店有A、B两种型号的童装,其进价与售价如下表所示:
型号 | 进价(元) | 售价(元) |
A型 | 90 | 108 |
B型 | 100 | 130 |
根据市场需要,服装店决定:购进A种服装的数量要比购进B种服装的2倍还多4件,且A种服装购进数量不超过28件,并使这批服装全部销售完毕后的总利润不少于699元.若假设购进B种服装x件,那么:
(1)请写出A、B两种服装全部销售完毕后的总利润y/元用含x/件的式子表示;
(2)请问该服装店有几种满足条件的进货方案?哪种方案获利最多?