Question

【题目】如图，已知△ABC中，∠ABC=45°，点D是BC边上一动点（与点B，C不重合），点E与点D关于直线AC对称，连结AE，过点B作BF⊥ED的延长线于点F．

（1）依题意补全图形；

（2）当AE=BD时，用等式表示线段DE与BF之间的数量关系，并证明．

Answer 1

【答案】（1）见解析;（2）结论：DE=2BF．理由见解析.

【解析】

（1）根据题意画出图形即可；

（2）结论：DE=2BF．连接AD，设DE交AC于H．想办法证明△ADH≌△DBF即可解决问题；

解：（1）依题意补全图形如图所示：

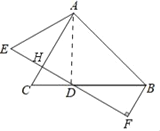
（2）结论：DE=2BF．

理由：连接AD，设DE交AC于H．

∵点E、D关于AC对称，

∴AC垂直平分DE．

∴AE=AD．

∵AE=BD，∴AD=DB．

∴∠DAB=∠ABC=45°．

∴∠ADC=90°．

∴∠ADE+∠BDF=90°．

∵BF⊥ED，AC⊥ED，

∴∠F=∠AHD=90°．

∴∠DBF+∠BDF=90°．

∴∠DBF=∠ADH．

∴△ADH≌△DBF

∴DH=BF

又∵DH=EH，

∴DE=2BF．