题目内容
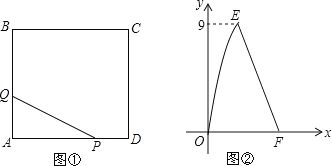
【题目】如图①，在正方形ABCD中，点P沿边DA从点D开始向点A以1
的速度移动，同时点Q沿边AB，BC从点A开始向点C以2的速度移动，当点P移动到点A时，P、Q同时停止移动.设点P出发
秒时，△PAQ的面积为
，
与的函数图像如图②，则下列四个结论：①当点P移动到点A时，点Q移动到点C；②正方形边长为6cm；③当AP=AQ时，△PAQ面积达到最大值；④线段EF所在的直线对应的函数关系式为
，其中正确的有（ ）
A.1个B.2个C.3个D.4个
【答案】C
【解析】
利用速度之间的关系可判断①，利用当Q点到B点时的面积最大可判断②和③，利用待定系数法可判断④.
∵点P以1
的速度移动，同时点Q以2的速度移动，∴当点P移动到点A时，点Q移动到点C，故①正确；
由图像可知，当Q点到B点时的面积最大，设边长为a，则
，∴a=6，故②正确；
由图像可知，当Q点到B点时的面积最大时，AP=
AQ，故③错误；
∵6÷2=3秒，12÷2=6秒，∴E（3，9），F（6，0），设线段EF所在的直线对应的函数关系式为y=kx+b，则
，解得
，∴ 
，故④正确.
故选C.
练习册系列答案
相关题目
【题目】.鞋子的“鞋码”和鞋长（cm）存在一种换算关系，下表是几组
“鞋码”与鞋长换算的对应数值：［注：“鞋码”是表示鞋子大小的一种号码］
鞋长（cm） | 16 | 19 | 21 | 24 |
鞋码（号） | 22 | 28 | 32 | 38 |
（1）设鞋长为x，“鞋码”为y，试判断点（x，y）在你学过的哪种函数的图象上？
（2）求x、y之间的函数关系式；（3）如果某人穿44号“鞋码”的鞋，那么他的鞋长是多少？
