题目内容
【题目】如图1,抛物线![]() 与两条坐标轴分别交于
与两条坐标轴分别交于![]() ,
,![]() ,
,![]() 三点.其中
三点.其中![]() ,且
,且![]() .
.
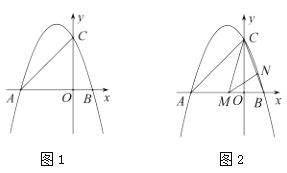
(1)求该抛物线的解析式;
(2)点![]() 是
是![]() 轴上一点,抛物线上是否存在点
轴上一点,抛物线上是否存在点![]() ,使得以点
,使得以点![]() ,
,![]() ,
,![]() ,
,![]() 为顶点,以
为顶点,以![]() 为边的四边形是平行四边形?若存在,求出点
为边的四边形是平行四边形?若存在,求出点![]() 的坐标;若不存在,请说明理由;
的坐标;若不存在,请说明理由;
(3)如图2,点![]() ,
,![]() 分别是线段
分别是线段![]() ,
,![]() 上的动点,连接
上的动点,连接![]() ,
,![]() ,当
,当![]() 时,求点
时,求点![]() 的坐标.
的坐标.
【答案】(1)![]() ;(2)存在,
;(2)存在,![]() ,
,![]() ,
,![]() ;(3)
;(3)![]()
【解析】
(1)根据![]() ,且
,且![]() ,得到点A的坐标,代入A和C的坐标即可求解;
,得到点A的坐标,代入A和C的坐标即可求解;
(2)该平行四边形以点![]() ,
,![]() ,
,![]() ,
,![]() 为顶点,以
为顶点,以![]() 为边,且Q在x轴上,设点
为边,且Q在x轴上,设点![]() 的坐标为
的坐标为![]() ,根据平行四边形的性质可得
,根据平行四边形的性质可得![]() ,求解即可;
,求解即可;
(3)由![]() 得到
得到![]() 平分
平分![]() ,故过点
,故过点![]() 分别作
分别作![]() 于
于![]() ,
,![]() 于
于![]() ,可得
,可得![]() ,并可用含m的代数式表示线段长度,通过证明得到
,并可用含m的代数式表示线段长度,通过证明得到![]() ,对应线段成比例可求得m的值,再证明
,对应线段成比例可求得m的值,再证明![]() ,并表示各自的正切值,即可求解.
,并表示各自的正切值,即可求解.
(1)∵![]() ,∴
,∴![]() ,
,
∵![]() ,
,
∴![]()
代入可得:![]() ,
,
解得:![]() ,∴
,∴![]() .
.
(2)存在,设点![]() 的坐标为
的坐标为![]() ,依题意有
,依题意有
![]()
当![]() 时,解得
时,解得![]() ,
,![]() (舍去),
(舍去),
∴![]()
当![]() 时,解得
时,解得![]() ,
,![]() ,
,
∴![]() ,
,![]() ,
,
(3)抛物线![]() ,
,
当![]() 时,
时,![]() ,解得:
,解得:![]() ,
,![]() ,∴
,∴![]() ,
,
∵![]() ,∴
,∴![]() ,
,![]() ,∴
,∴![]() 平分
平分![]() ,
,
过点![]() 分别作
分别作![]() 于
于![]() ,
,![]() 于
于![]() ,∴
,∴![]()
∵![]() ,∴
,∴![]() ,
,
∴![]() 是等腰直角三角形,
是等腰直角三角形,
设![]() ,则
,则![]() ,
,![]() ,
,
∴![]() ,
,
∵![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,即
,即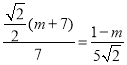 ,
,
解得:![]() ,∴
,∴![]() ,
,
设直线![]() 的解析式为
的解析式为![]() ,易得
,易得![]() ,
,
![]() ,过点
,过点![]() 作
作![]() 轴于
轴于![]() .
.
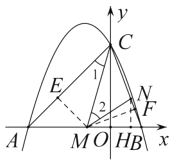
∵![]() ,
,![]() ,∴
,∴![]() ,
,
∵ ,
,
∴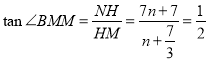 ,
,
解得:![]() ,
,![]() ,
,
∴![]() .
.

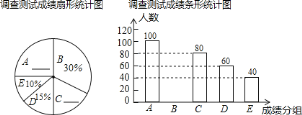
【题目】4月23日是世界读书日,校文学社为了解学生课外阅读的情况,抽样调查了部分学生每周用于课外阅读的时间,过程如下:
收集数据:从学校随机抽取20名,进行了每周用于课外阅读时间的调查,数据如下(单位:![]() ):
):
30 | 60 | 81 | 50 | 40 | 110 | 130 | 146 | 90 | 100 |
60 | 81 | 120 | 140 | 70 | 81 | 10 | 20 | 100 | 81 |
整理数据:按如下分数段整理样本数据并补全表格:
|
|
|
| |
等级 |
|
|
|
|
人数 | 3 |
| 8 | 4 |
分析数据:补全下列表格中的统计量:
平均数 | 中位数 | 众数 |
80 |
|
|
得出结论:
(1)请写出表中![]() _________;
_________;![]() _________
_________![]() ;
;![]() __________
__________![]() ;
;
(2)如果该校现有学生7500人,估计等级为“![]() ”的学生有_________名;
”的学生有_________名;
(3)假设平均阅读一本课外书的时间为![]() ,请你选择一种统计量估计该校学生每人一年(按52周计算)平均阅读多少本课外书?
,请你选择一种统计量估计该校学生每人一年(按52周计算)平均阅读多少本课外书?