题目内容
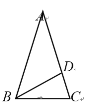
【题目】如图，在△ABC中，∠A=36°，AB=AC，BD平分∠ABC，则图中等腰三角形的个数是（ ）
A.0个B.1个C.2个D.3个
【答案】D
【解析】
利用等腰三角形的定义得到△ABC为等腰三角形，再根据等腰三角形的性质和三角形内角和计算出∠ABC＝∠C＝72°，接着根据角平分线的定义得到∠ABD＝∠CBD＝36°，然后判断△ABD和△BDC为等腰三角形．
解：∵AB＝AC，
∴△ABC为等腰三角形，
∴∠ABC＝∠C＝
（180°﹣∠A）＝（180°﹣36°）＝72°，
∵BD平分∠ABC，
∴∠ABD＝∠CBD＝×72°＝36°，
∴∠ABD＝∠A，
∴△ABD为等腰三角形，
∵∠BDC＝∠A+∠ABD＝72°，
∴∠BDC＝∠C，
∴△BDC为等腰三角形．
故选：D．
练习册系列答案
相关题目
【题目】为贯彻落实省教育厅提出的“三生教育”．在母亲节来临之际，某校团委组织了以“珍爱生命，
学会生存，感恩父母”为主题的教育活动，在学校随机调查了50名同学平均每周在家做家务的时间，统
计并制作了如下的频数分布表和扇形统计图：
组别 | 做家务的时间 | 频数 | 频率 |
A | 1≤t＜2 | 3 | 0.06 |
B | 2≤t＜4 | 20 | 0.40 |
C | 4≤t＜6 | a | 0.30 |
D | 6≤t＜8 | 8 | b |
E | t≥8 | 4 | 0.08 |
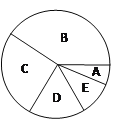
根据上述信息回答下列问题：
（1）a= ，b= ．
（2）在扇形统计图中，B组所占圆心角的度数为 ．
（3）全校共有2000名学生，估计该校平均每周做家务时间不少于4小时的学生约有多少人？
