��Ŀ����
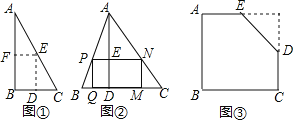
����Ŀ����ͼ�٣���һ��ֱ��������ֽƬ����B��90����AB��12��BC��8��С������м���һ���ԡ�BΪ�ڽ���������ľ��Σ������������֣���������λ��DE��EF����ʱ�����õľ��ε�������
��1����ͨ������˵��С���IJ����Ƿ���ȷ��
��2����ͼ�ڣ��ڡ�ABC�У�BC��10��BC���ϵĸ�AD��10������PQMN�Ķ���P��N�ֱ��ڱ�AB��AC�ϣ�����Q��M�ڱ�BC�ϣ������PQMN��������ֵ��
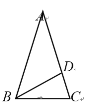
��3����ͼ�ۣ��������ABCDE�У�AB��16��BC��20��AE��10��CD��8����A����B����C��90����С�����м�����һ��������ľ��Σ���BΪ���������ε��ڽǣ�����þ��ε������
���𰸡���1����ȷ�����ɼ���������2����a��5ʱ��S����MNPQ���Ϊ25����3�����ε�������Ϊ180��
��������
(1)��BF=x����AF=12��x��֤����AFE�ס�ABC��������ʾ��EF�����������ʽ�ó�S����BDEF=��![]() (x��6)2+24�����ɵó����ۣ�
(x��6)2+24�����ɵó����ۣ�
(2)��DE=a��AE=10��a����֤����APN�ס�ABC�������ó�PN=10��a�����������ʽS����MNPQ=��(a��5)2+25�����ɵó������
(3)�ӳ�BA��DE���ڵ�F���ӳ�BC��ED���ڵ�G���ӳ�AE��CD���ڵ�H��ȡBF�е�I��FG���е�K������IK������K��KL��BC��L���ɾ�������֪AE=EH=10��CD=DH=8���ֱ�֤��AEF�ա�HED����CDG�ա�HDE��AF=DH=8��CG=HE=10���Ӷ��жϳ���λ��IK�����˵����߶�AB��DE�ϣ�����(1)�Ľ��۽�ɣ�
(1)��ȷ�����ɣ�
��BF=x(0��x��12)��
��AB=12��
��AF=12��x��
����F��FE��BC��AC��E������E��ED��AB��BC��D��
���ı���BDEF��ƽ���ı��Σ�
�ߡ�B=90����
��BDEF�Ǿ��Σ�
��EF��BC��
���AFE�ס�ABC��
��![]() =
=![]() ��
��
��![]() ��
��
��EF=![]() (12��x)��
(12��x)��
��S����BDEF=EFBF=![]() (12��x)x=��
(12��x)x=��![]() (x��6)2+24
(x��6)2+24
�൱x=6ʱ��S����BDEF���=24��
��BF=6��AF=6��
��AF=BF��
�൱������λ��DE��EF����ʱ�����õľ��ε�������
(2)��DE=a��(0��a��10)��
��AD=10��
��AE=10��a��
���ı���MNPQ�Ǿ��Σ�
��PQ=DE=a��PN��BC��
���APN�ס�ABC��
��![]() =
=![]() ��
��
��![]() =
=![]() ��
��
��PN=10��a��
��S����MNPQ=PNPQ=(10��a)a=��(a��5)2+25��
�൱a=5ʱ��S����MNPQ���Ϊ25��
(3)�ӳ�BA��DE���ڵ�F���ӳ�BC��ED���ڵ�G���ӳ�AE��CD���ڵ�H��ȡBF�е�I��FG���е�K������IK������K��KL��BC��L����ͼ����ʾ��
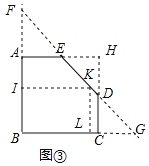
�ߡ�A=��HAB=��BCH=90����
���ı���ABCH�Ǿ��Σ�
��AB=16��BC=20��AE=10��CD=8��
��EH=10��DH=8��
��AE=EH��CD=DH��
�ڡ�AEF�͡�HED�У�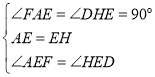 ��
��
���AEF�ա�HED(ASA)��
��AF=DH=8��
��BF=AB+AF=16+8=24��
ͬ����CDG�ա�HDE��
��CG=HE=10��
��BG=BC+CG=20+10=30��
��BI=![]() BF=12��
BF=12��
��BI=12��16��
����λ��IK�����˵����߶�AB��DE�ϣ�
��IK=![]() BG=15��
BG=15��
��(1)֪���ε�������ΪBIIK=12��15=180��