��Ŀ����
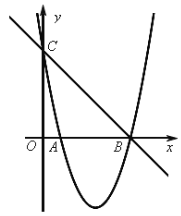
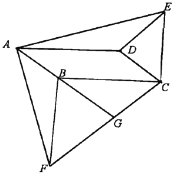
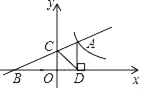
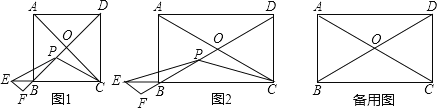
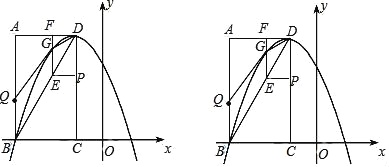
����Ŀ����ͼ����ƽ��ֱ������ϵ�У���֪����ABCD����������A(��3��4)��B(��3��0)��C(��1��0)����DΪ�����������y��ax2+bx+c����B������P�ӵ�D��������DC�����C�˶���ͬʱ����Q�ӵ�B��������BA�����A�˶�����P��Q�˶����ٶȾ�Ϊÿ��1����λ���˶���ʱ��Ϊt�룮����P��PE��CD��BD�ڵ�E������E��EF��AD�ڵ�F�����������ڵ�G��
(1)�������ߵĽ���ʽ��
(2)��tΪ��ֵʱ���ı���BDGQ�����������ֵΪ���٣�
(3)����P��Q�˶������У��Ƿ����ijһʱ�̣�ʹ��PQF�ǵ��������Σ������ڣ��������ʱt��ֵ���������ڣ���˵�����ɣ�
���𰸡�(1)y����x2��2x+3��(2)��t��2ʱ��S�����ֵΪ2��(3)���ڣ�t��![]() ��
��![]() ��2��
��2��
��������
(1)�������D�����꣬�趥��ʽ�������B�����꼴����������ߵĽ���ʽ��
(2)���ݶ�����˶��ٶȣ��ֱ��ʾ��EG��BQ��AF��EP�ij��ȣ���ʾS���䷽����ֵ���ɣ�
(3)�ֱ��ʾ��P��Q��F�����꣬���������빫ʽ��ʾ�߶γ��ȣ�������������ۼ��ɣ�
�⣺(1)��A(��3��4)��B(��3��0)��C(��1��0)��
��D(��1��4)��
���������ߵĽ���ʽΪy��a(x+1)2+4�������B��
0��a(��3+1)2+4��
���a����1��
�������ߵĽ���ʽΪy����x2��2x+3��
(2)�������֪��DP��BQ��t��
��tan��BDC��![]() ��
��
��EP��![]() t��
t��
��G�ĺ�����Ϊ��1��![]() t��
t��
��G(��1��![]() t��4��
t��4��![]() )��
)��
��EG��t��![]() ��
��
S��DGE��(t��![]() )
)![]()
![]() ��
��![]() ��
��![]() ��
��
SQBEG��(t��![]() +t)(2��
+t)(2��![]() )
)![]() ��
��![]() ��
��
��S��2t��![]() ����
����![]() (t��2)2+2��
(t��2)2+2��
�ߩ�![]() ��0��
��0��
�൱t��2ʱ��S�����ֵΪ2��
(3)��P(��1��4��t)��Q(��3��t)��F(��1��![]() ��4)��
��4)��
��PQ��![]() ��PF��
��PF��![]() ��QF��
��QF��![]() ��
��
��PQ��PF��
![]() ��
��
���t1��4(��)��t2��![]() ��
��
��PQ��QF��
![]() ��
��
���t1��0(��)��t2��![]() ��
��
��PF��QF��
![]() ��
��
���t��2��
����������t��![]() ��
��![]() ��2��
��2��

����Ŀ��ijУ�ƻ������ס������ֹ�����ܣ����г����鷢�������Ϻ��������ֹ���ʽ������������±���
��� | ���� | ���� | ||
����(Ԫ/��) | �˷�(Ԫ/��) | ����(Ԫ/��) | �˷�(Ԫ/��) | |
�� | 240 | 0 | 210 | 20 |
�� | 300 | 0 | 250 | 30 |
(1)��������¹���ס���������ܹ�30��������8280Ԫ����ס���������ܸ������˶��ٸ���
(2)��������Ϲ���ס���������ܹ�30�����ҹ���������ܵ����������ڼ�����ܵ�3����������������ٵĹ��������ѣ�