��Ŀ����
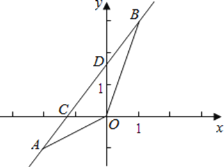
����Ŀ����ͼ����֪������![]() ��ͼ����x���һ������ΪB��5��0������һ������ΪA������y�ύ�ڵ�C��0��5����
��ͼ����x���һ������ΪB��5��0������һ������ΪA������y�ύ�ڵ�C��0��5����
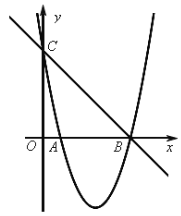
��1����ֱ��BC�������ߵĽ���ʽ��
��2������M����������x���·�ͼ���ϵĶ��㣬����M��MN��y����ֱ��BC�ڵ�N����MN�����ֵ��
��3���ڣ�2���������£�MNȡ�����ֵʱ������P����������x���·�ͼ��������һ�㣬��BCΪ����ƽ���ı���CBPQ����ƽ���ı���CBPQ�����ΪS1����ABN�����ΪS2����S1=6S2�����P�����ꡣ
���𰸡��⣺��1����ֱ��BC�Ľ���ʽΪ![]() ��
��
��B��5��0����C��0��5�����룬��![]() ����
����![]() ��
��
��ֱ��BC�Ľ���ʽΪ![]() ��
��
��B��5��0����C��0��5������![]() ����
����![]() ����
����![]() ��
��
�������ߵĽ���ʽ![]() ��
��
��2������M����������x���·�ͼ���ϵĶ��㣬����M![]() ��
��
����N��ֱ��BC�����M��������ͬ�ĵ㣬��N![]() ��
��
������M����������x���·�ʱ��N���������ܴ���M�������ꡣ
��![]() ��
��
��MN�����ֵ��![]() ��
��
��3����MNȡ�����ֵʱ��N![]() ��
��
��![]() �ĶԳ�����
�ĶԳ�����![]() ��B��5��0������A��1��0������AB=4��
��B��5��0������A��1��0������AB=4��
��![]() ��
��
�ɹ��ɶ����ɵã�![]() ��
��
��BC��PQ�ľ���Ϊh������S1=6S2�ã�![]() ����
����![]() ��
��
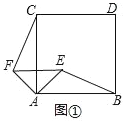
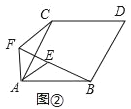
��ͼ������B��ƽ���ı���CBPQ�ĸ�BH������H��x��Ĵ��߽���E ����BH=![]() ��EH��ֱ��BC��y�᷽��ƽ�Ƶľ��롣
��EH��ֱ��BC��y�᷽��ƽ�Ƶľ��롣
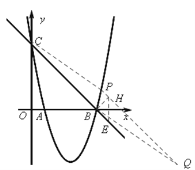
�ã���BEH�ǵ���ֱ�������Σ�
��EH=![]() ��
��
��ֱ��BC��y�᷽��ƽ��6����λ��PQ�Ľ���ʽ��
![]() ��
��![]() ��
��
��![]() ʱ����
ʱ����![]() ��������
��������
![]() �����
�����![]() ��
��![]() ����ʱ����P������Ϊ����1��12����6��5����
����ʱ����P������Ϊ����1��12����6��5����
��![]() ʱ����
ʱ����![]() ��������
��������
![]() �����
�����![]() ��
��![]() ����ʱ����P������Ϊ��2����3����3����4����
����ʱ����P������Ϊ��2����3����3����4����
������������P����������1��12����6��5����2����3����3����4����
����������1����B��5��0����C��0��5����Ӧ�ô���ϵ����������ֱ��BC�������ߵĽ���ʽ��
��2������MN���ڵ�M������ĺ�����ϵʽ��Ӧ�ö��κ�����ֵԭ�������
��3������S1=6S2���BC��PQ�ľ���h���Ӷ����PQ��BCƽ�Ƶľ��룬����ƽ�Ƶ��������PQ�Ľ���ʽ����������![]() ���������������P�����ꡣ
���������������P�����ꡣ

����Ŀ��ijУ���꼶�����࣬��ѡ��10��ѧ���μ�ѧУ���е�������������������֪ʶ������Ԥ��������ѡ�ֵijɼ����£�
�ˣ�1���ࣺ88��91��92��93��93��93��94��98��98��100��
�ˣ�2���ࣺ89��93��93��93��95��96��96��98��98��99��
ͨ���������õ����ݷ��������£�
�༶ | ��߷� | ƽ���� | ��λ�� | ���� | ���� |
�ˣ�1���� | 100 | m | 93 | 93 | 12 |
�ˣ�2���� | 99 | 95 | n | 93 | 8.4 |
��1�������m��n��ֵ��
��2���������ݷ���������ͬѧ˵������߷��ڣ�1���࣬��1����ijɼ��ȣ�2�����������Ҳ��ͬѧ˵��2����ijɼ���������д������֧�ְˣ�2����ɼ��õ����ɣ�