题目内容
【题目】已知:菱形 ABCD,点 E 在线段 BC 上,连接 DE,点 F 在线段 AB 上,连接 CF、DF, CF 与 DE 交于点 G,将菱形 ABCD 沿 DF 翻折,点 A 恰好落在点 G 上.
(1)求证:CD=CF;
(2)设∠CED= x,∠DCF= y,求 y 与 x 的函数关系式;(不要求写出自变量的取值范围)
(3)在(2)的条件下,当 x=45°时,以 CD 为底边作等腰△CDK,顶角顶点 K 在菱形 ABCD的内部,连接 GK,若 GK∥CD,CD=4 时,求线段 KG 的长.


【答案】(1)见解析;(2)y=![]() ;(2)
;(2)![]()
【解析】
(1)根据翻折的性质得△DFG≌△DFA,从而推导得出∠FDC=∠DFG,进而得到CF=DC;
(2)在等腰△DGC和等腰△CFD中,可用y表示出∠GDC、∠FDC的值,从而求出∠ADF,根据∠ADE=∠DEC,得出y与x的关系式;
(3)先证△KCD是等腰直角三角形,根据CD的长得到KC的值,然后再△KGC中求得KG的值.
(1)∵将菱形ABCD沿DF翻折,点A恰好落在点G上
∴△DFG≌△DFA,∠AFD=∠FDC
∴∠AFD=∠DFG
∴∠FDC=∠DFG
∴CF=DC;
(2)∵AD=DG=DC=FC,∠DCF=y
∴在△DGC中,∠DGC=y,∠GDC=180-2y
在△CFD中,∠CFD=∠CDF=![]()
∴∠FDG=∠FDC-∠GDC=![]()
∴∠ADF=∠FDG=![]() ,∴∠ADE=3y-180
,∴∠ADE=3y-180
∵AD∥BC
∴∠ADE=∠DEC,即3y-180=x
化简得:y=![]() ;
;
(3)如下图,过点K作CD的垂线,交CD于点I,延长KG交BC于点L,过点C作GL的垂线,交GL于点Q,过点C作GD的垂线,交GD于点N,
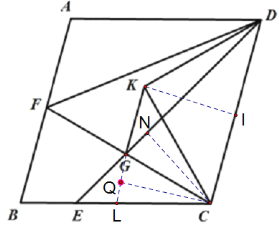
∵x=45°,
∴y=75°,∠ADE=x=45°
∴∠DGC=∠DCG=75°,
∴∠NDC=30°,
∴∠ADC=45°+30°=75°,
∵四边形ABCD是菱形,
∴∠B=75°,
∵KG∥DC,
∴KG∥AB,∠KGD=∠NDC=30°,
∴∠GLC=∠B=75°,∠KGC=30°+75°=105°,
∴∠LGC=75°,
∴∠CGL=∠CGN,
∴GC是∠LGN的角平分线,
∴CQ=CN,
∵CD=4,∠CDE=30°,
∴在Rt△CND中,CN=2,
∴CQ=2,
∵KG∥CD,
∴∠QKI=∠KIC=90°
∵CQ⊥KL
∴四边形CQKI是矩形,
∵CK=KD,KI⊥CD,
∴CI=ID=2,
∴CI=CQ=2,
∴矩形CQKI是正方形
∴IK=CQ=2,
∴在Rt△KIC中,CK=![]() ,
,
如下图,过点G作CK的垂线,交CK于点M,
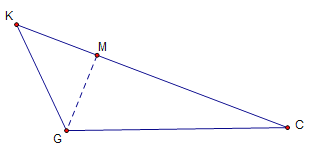
∴△KGM是等腰直角三角形,△GMC是直角三角形,且∠C=30°,
设GM=x,
则在Rt△GKM中,KM=GM=x,
在Rt△GMC中,CG=2x,MC=![]() x,
x,
∴KC=![]() x+x=
x+x=![]() ,
,
解得:x=![]() ,
,
∴KG=![]() .
.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案