题目内容
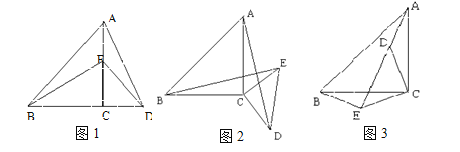
【题目】如图,四边形![]() 和
和![]() 都是正方形,点
都是正方形,点![]() 在
在![]() 边上,点
边上,点![]() 在对角线
在对角线![]() 上,若
上,若![]() ,则
,则![]() 的面积是( )
的面积是( )
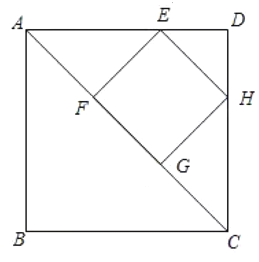
A.6B.8C.9D.12
【答案】B
【解析】
根据正方形的性质得到∠DAC=∠ACD=45°,由四边形EFGH是正方形,推出△AEF与△DFH是等腰直角三角形,于是得到DE=![]() EH=
EH=![]() EF,EF=
EF,EF=![]() AE,即可得到结论.
AE,即可得到结论.
解:∵在正方形ABCD中,∠D=90°,AD=CD=AB,
∴∠DAC=∠DCA=45°,
∵四边形EFGH为正方形,
∴EH=EF,∠AFE=∠FEH=90°,
∴∠AEF=∠DEH=45°,
∴AF=EF,DE=DH,
∵在Rt△AEF中,AF2+EF2=AE2,
∴AF=EF=![]() AE,
AE,
同理可得:DH=DE=![]() EH
EH
又∵EH=EF,
∴DE=![]() EF=
EF=![]() ×
×![]() AE=
AE=![]() AE,
AE,
∵AD=AB=6,
∴DE=2,AE=4,
∴EH=![]() DE=2
DE=2![]() ,
,
∴![]() 的面积为EH2=(2
的面积为EH2=(2![]() )2=8,
)2=8,
故选:B.

练习册系列答案
相关题目