题目内容
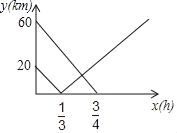
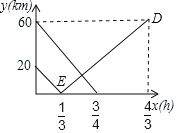
【题目】在连接A、B两市的公路之间有一个机场C,机场大巴由A市驶向机场C,货车由B市驶向A市,两车同时出发匀速行驶,图中线段、折线分别表示机场大巴、货车到机场C的路程y(km)与出发时间x(h)之间的函数关系图象.
(1)直接写出连接A、B两市公路的路程以及货车由B市到达A市所需时间.
(2)求机场大巴到机场C的路程y(km)与出发时间x(h)之间的函数关系式.
(3)求机场大巴与货车相遇地到机场C的路程.
【答案】(1)连接A、B两市公路的路程为80km,货车由B市到达A市所需时间为![]() h;(2)y=﹣80x+60(0≤x≤
h;(2)y=﹣80x+60(0≤x≤![]() );(3)机场大巴与货车相遇地到机场C的路程为
);(3)机场大巴与货车相遇地到机场C的路程为![]() km.
km.
【解析】分析:(1)根据![]() 可求出连接A、B两市公路的路程,再根据货车
可求出连接A、B两市公路的路程,再根据货车![]() h行驶20km可求出货车行驶60km所需时间;
h行驶20km可求出货车行驶60km所需时间;
(2)根据函数图象上点的坐标,利用待定系数法即可求出机场大巴到机场C的路程y(km)与出发时间x(h)之间的函数关系式;
(3)利用待定系数法求出线段ED对应的函数表达式,联立两函数表达式成方程组,通过解方程组可求出机场大巴与货车相遇地到机场C的路程.
详解:(1)60+20=80(km),
![]() (h).
(h).
∴连接A.B两市公路的路程为80km,货车由B市到达A市所需时间为![]() h.
h.
(2)设所求函数表达式为y=kx+b(k≠0),
将点(0,60)、![]() 代入y=kx+b,
代入y=kx+b,
得: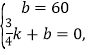 解得:
解得:![]()
∴机场大巴到机场C的路程y(km)与出发时间x(h)之间的函数关系式为![]()
(3)设线段ED对应的函数表达式为y=mx+n(m≠0),
将点![]() 代入y=mx+n,
代入y=mx+n,
得: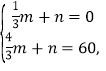 解得:
解得:![]()
∴线段ED对应的函数表达式为![]()
解方程组![]() 得
得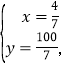
∴机场大巴与货车相遇地到机场C的路程为![]() km.
km.

练习册系列答案
相关题目