��Ŀ����
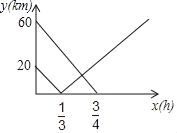
����Ŀ����ͼ��ֱ��AB��y��![]() x+2��x�ᡢy��ֱ���A��B���㣬C�ǵ�һ������ֱ��AB��һ�㣬����C��CD��x���ڵ�D����CD�ij�Ϊ
x+2��x�ᡢy��ֱ���A��B���㣬C�ǵ�һ������ֱ��AB��һ�㣬����C��CD��x���ڵ�D����CD�ij�Ϊ![]() ��P��x���ϵĶ��㣬N��ֱ��AB�ϵĶ��㣮
��P��x���ϵĶ��㣬N��ֱ��AB�ϵĶ��㣮
��1��ֱ��д��A��B��������ꣻ
��2����ͼ��������M������Ϊ��0��![]() �����Ƿ����������P�㣮ʹ��O��P��M��NΪ������ı�����ƽ���ı��Σ������ڣ������P�����ꣻ�������ڣ���˵�����ɣ�
�����Ƿ����������P�㣮ʹ��O��P��M��NΪ������ı�����ƽ���ı��Σ������ڣ������P�����ꣻ�������ڣ���˵�����ɣ�
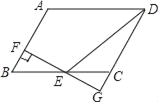
��3����ͼ������ֱ��AB�Ƶ�C��ʱ����ת��y���ڵ�F����x���ڵ�E������ת�Ǽ���ACE��45�㣬���BFC�������
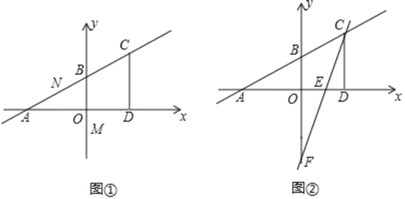
���𰸡���1����A����4��0������B��0��2������2����P����1��0����7��0����7��0������3��S��BFC��![]() .
.
��������
��1����x��0��y��0�����A����B���ꣻ
��2����OMΪ�ߣ�OMΪ�Խ�������������ۣ���ƽ���ı��ε����ʿ����P���ꣻ
��3������C��CG��AB����x���ڵ�G��������ɵõ�C���꣬������ֱ��CG����ʽΪ��y��2x��![]() ���ɵõ�G���꣬��������Ǻ����ͽ�ƽ���ߵ����ʿɵ�
���ɵõ�G���꣬��������Ǻ����ͽ�ƽ���ߵ����ʿɵ�![]() �������E���꣬�ô���ϵ��������ֱ��CF����ʽ�������F���꣬��������BFC�������
�������E���꣬�ô���ϵ��������ֱ��CF����ʽ�������F���꣬��������BFC�������
��1����x��0ʱ��y��2��
��y��0ʱ��0��![]() ��x+2
��x+2
��x����4
���A����4��0������B��0��2��
�ʴ�Ϊ������4��0������0��2��
��2�����P��x��0��
��OMΪ�ߣ���OM��PN��OM��PN
�ߵ�M������Ϊ��0�� ![]() ����
����
��OM��x�ᣬOM��![]()
��PN��x�ᣬPN��![]()
�൱y��![]() ʱ����
ʱ����![]() ��
��![]() x+2
x+2
��x����1
��y����![]() ʱ����
ʱ����![]() ��
��![]() x+2
x+2
��x����7
���P����1��0������P����7��0��
��OMΪ�Խ��ߣ���OM��PN����ƽ�֣�
�ߵ�M������Ϊ��0��![]() ������O�����꣨0��0��
������O�����꣨0��0��
��OM���е����꣨0��![]() ��
��
�ߵ�P��x��0����
���N����x��![]() ��
��
��![]() ��
��![]() ������x��+2
������x��+2
��x��7
���P��7��0��
������������P����1��0����7��0����7��0��
��3����CD��![]() ������C������Ϊ
������C������Ϊ![]() ��
��
��![]() ��
��![]() x+2
x+2
��x��3
���C��3��![]() ��
��
��ͼ������C��CG��AB����x���ڵ�G��
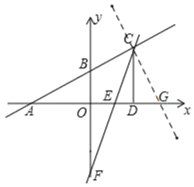
��CG��AB��
����ֱ��CG����ʽΪ��y����2x+b
��![]() ����2��3+b
����2��3+b
��b��![]()
��ֱ��CG����ʽΪ��y����2x+![]() ,
,
���G������![]() ��0��
��0��
�ߵ�A����4��0������B��0��2��
��OA��4��OB��2��AG��![]()
��tan��CAG��![]()
��![]()
�ߡ�ACF��45������ACG��90��
���ACF����FCG��45��
��![]() ����AE+EG��
����AE+EG��![]()
��AE��![]()
��OE��AE��AO��![]()
���E������![]() ��0��
��0��
��ֱ��CE����ʽΪ��y��mx+n
��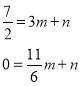
��ã�m��3��n��![]()
��ֱ��CE����ʽΪ��y��3x![]()
�൱x��0ʱ��y��![]()
���F��0��![]() ��
��
��BF��![]()
��S��BFC��![]() .
.

 ���ſ����ϵ�д�
���ſ����ϵ�д� ���Ŀ����ϵ�д�
���Ŀ����ϵ�д� ������ӱ������ͯ������ϵ�д�
������ӱ������ͯ������ϵ�д�