题目内容
【题目】抛物线
与x轴交于A，B两点（点A在点B左侧），与y轴交于点C，点D为顶点．
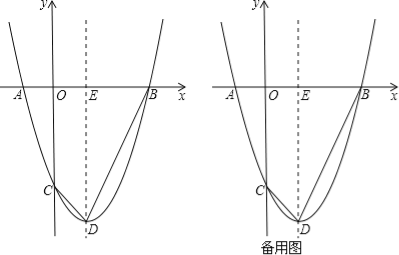
（1）求点B及点D的坐标．
（2）连结BD，CD，抛物线的对称轴与x轴交于点E．
①若线段BD上一点P，使∠DCP=∠BDE，求点P的坐标．
②若抛物线上一点M，作MN⊥CD，交直线CD于点N，使∠CMN=∠BDE，求点M的坐标．
【答案】（1）B的坐标为（3，0） D的坐标为（1，－4）
（2）①点P的坐标为（
，
）②点M坐标为（
）或（5，12）
【解析】
解：（1）∵抛物线
与x轴交于A，B两点（点A在点B左侧），
∴当y=0时，
，解得x=3或x=﹣1．∴点B的坐标为（3，0）．
∵
，∴顶点D的坐标为（1，－4）．
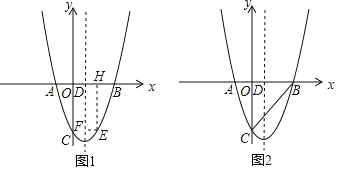
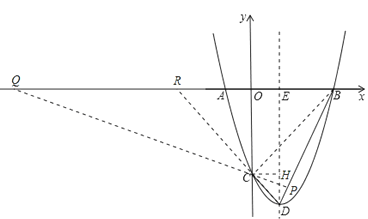
（2）①如图，
∵抛物线与y轴交于点C，
∴C点坐标为（0，－3）．
∵对称轴为直线x=1，
∴点E的坐标为（1，0）．
连接BC，过点C作CH⊥DE于H，则H点坐标为（1，﹣3），
∴CH=DH=1．
∴∠CDH=∠BCO=∠BCH=45°．
∴CD=
，CB=3，△BCD为直角三角形．
分别延长PC、DC，与x轴相交于点Q，R．
∵∠BDE=∠DCP=∠QCR，
∠CDB=∠CDE+∠BDE=45°+∠DCP，∠QCO=∠RCO+∠QCR=45°+∠DCP，
∴∠CDB=∠QCO．∴△BCD∽△QOC．∴
．
∴OQ=3OC=9，即Q（﹣9，0）.
∴直线CQ的解析式为
．
又直线BD的解析式为
，
由方程组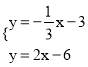
解得：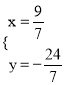
．
∴点P的坐标为（，）．
②（Ⅰ）当点M在对称轴右侧时，
若点N在射线CD上，如图，
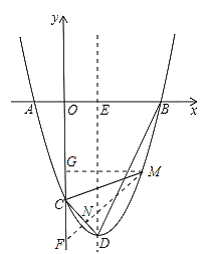
延长MN交y轴于点F，过点M作MG⊥y轴于点G．，
∵∠CMN=∠BDE，∠CNM=∠BED=90°，
∴△MCN∽△DBE．∴
．∴MN=2CN．
设CN=a，则MN=2a．
∵∠CDE=∠DCF=45°，
∴△CNF，△MGF均为等腰直角三角形．
∴NF=CN=a，CF=a．∴MF=MN+NF=3a．∴MG=FG=
a．
∴CG=FG﹣FC=
a．
∴M（a，
）．
代入抛物线，解得a=
．，
∴M（）．
若点N在射线DC上，如图，
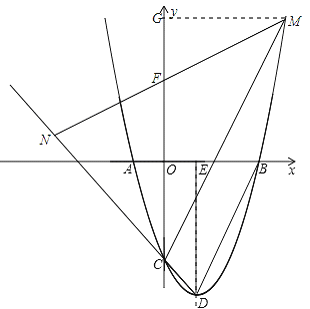
MN交y轴于点F，过点M作MG⊥y轴于点G，
∵∠CMN=∠BDE，∠CNM=∠BED=90°，
∴△MCN∽△DBE，∴．
∴MN=2CN．．
设CN=a，则MN=2a．
∵∠CDE=45°，
∴△CNF，△MGF均为等腰直角三角形．，
∴NF=CN=a，CF=a．
∴MF=MN﹣NF=a，∴MG=FG=a．∴CG=FG+FC=a．∴M（a，
）．
代入抛物线，解得a=
．
∴M（5，12）．
（Ⅱ）当点M在对称轴左侧时，
∵∠CMN=∠BDE＜45°，∴∠MCN＞45°．
而抛物线左侧任意一点K，都有∠KCN＜45°，∴点M不存在．
综上可知，点M坐标为（）或（5，12）．
（1）解方程，求出x=3或﹣1，根据抛物线与x轴交于A，B两点（点A在点B左侧），确定点B的坐标为（3，0）；将抛物线写成顶点式
，即可确定顶点D的坐标．
（2）①根据抛物线，得到点C、点E的坐标．连接BC，过点C作CH⊥DE于H，由勾股定理得出CD=，CB=3，证明△BCD为直角三角形．分别延长PC、DC，与x轴相交于点Q，R．根据两角对应相等的两三角形相似证明△BCD∽△QOC，则，得出Q的坐标（﹣9，0），运用待定系数法求出直线CQ的解析式为，直线BD的解析式为，解方程组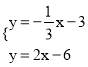，即可求出点P的坐标．
②分点M在对称轴右侧和点M在对称轴左侧两种情况进行讨论：（Ⅰ）当点M在对称轴右侧时，分点N在射线CD上和点N在射线DC上两种情况讨论；（Ⅱ）当点M在对称轴左侧时，由于∠BDE＜45°，得到∠CMN＜45°，根据直角三角形两锐角互余得出∠MCN＞45°，而抛物线左侧任意一点K，都有∠KCN＜45°，所以点M不存在．
一诺书业暑假作业快乐假期云南美术出版社系列答案
