��Ŀ����
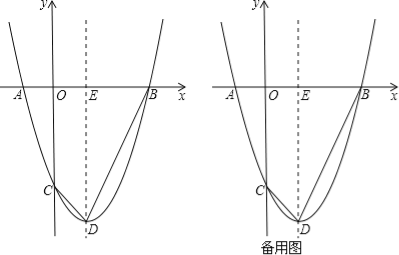
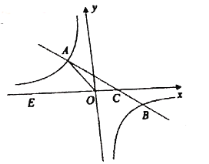
����Ŀ����ͼ1����ƽ��ֱ������ϵ![]() �У�һ�κ���
�У�һ�κ���![]() ��
��![]() �ᡢ
�ᡢ![]() �ύ�ڵ�
�ύ�ڵ�![]() ��
��![]() ���㣬
���㣬![]() ��ĸ�������һ��
��ĸ�������һ��![]() ��
��![]() �������������һ��
�������������һ��![]() ��
��![]()
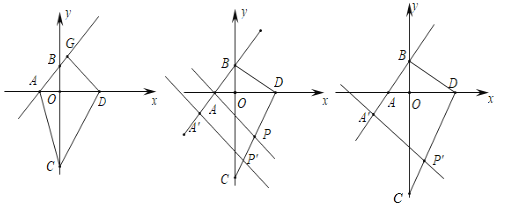
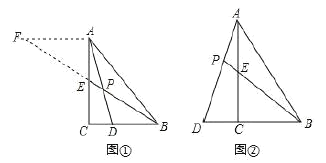
��1����ͼ1����ֱ��![]() ����һ��Ϊ
����һ��Ϊ![]() ���߶�
���߶�![]() ����
����![]() ʼ���ڵ�
ʼ���ڵ�![]() ����ࣩ�����߶�
����ࣩ�����߶�![]() ��ֱ��
��ֱ��![]() ƽ�Ƶõ��߶�
ƽ�Ƶõ��߶�![]() ��ʹ���ı���
��ʹ���ı���![]() ���ܳ���С��������ı���
���ܳ���С��������ı���![]() �ܳ�����Сֵ�ʹ�ʱ��
�ܳ�����Сֵ�ʹ�ʱ��![]() �����꣮
�����꣮
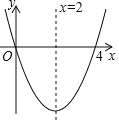
��2����ͼ2����![]() ��ֱ��
��ֱ��![]() ��ֱ��
��ֱ��![]() ��
��![]() �㣬��ֱ��
�㣬��ֱ��![]() ��ֱ��
��ֱ��![]() ƽ�ƣ�ƽ�ƺ���ֱ��
ƽ�ƣ�ƽ�ƺ���ֱ��![]() ��
��![]() �Ľ���ֱ���
�Ľ���ֱ���![]() ��
��![]() �����ʣ���ֱ��
�����ʣ���ֱ��![]() ���Ƿ����һ��
���Ƿ����һ��![]() ��ʹ
��ʹ![]() �ǵ��������Σ������ڣ������ʱ��������������
�ǵ��������Σ������ڣ������ʱ��������������![]() ������Ӧ��
������Ӧ��![]() �����ꣻ�������ڣ���˵�����ɣ�
�����ꣻ�������ڣ���˵�����ɣ�
���𰸡���1���ı���CDG'F'�ܳ�����СֵΪ3![]() +2
+2![]() +
+![]() ��G'��-7��1������2�����ڣ�A'��-2��-1����A'��-
��G'��-7��1������2�����ڣ�A'��-2��-1����A'��-![]() ��-
��-![]() ����A'��1+
����A'��1+![]() ��2+
��2+![]() ����A'��-2-
����A'��-2-![]() ��-1-
��-1-![]() ��
��
��������
��1��������ɵã�A��-1��0����B��0��1����C��0��-6����D��3��0��������D��DN��AB������F'��F'N��DG'������C����ֱ��AB�ĶԳƵ�G'������G'N��AB�Ľ���ΪF'����ʱG'D=F'N��G'F'=F'C���ı���CDG'F'�ܳ�=CD+F'G'+CF'+G'D=3![]() +2
+2![]() +F'G'+F'N=3
+F'G'+F'N=3![]() +2
+2![]() +G'N�����AB�Ľ���ʽΪy=x+1��DN��ֱ�߽���ʽΪy=x-3�����N��1��-2����G'��-7��1������G'N=
+G'N�����AB�Ľ���ʽΪy=x+1��DN��ֱ�߽���ʽΪy=x-3�����N��1��-2����G'��-7��1������G'N=![]() �������ı���CDG'F'�ܳ�����СֵΪ3
�������ı���CDG'F'�ܳ�����СֵΪ3![]() +2
+2![]() +
+![]() ��
��
��2�������CD��ֱ�߽���ʽΪy=2x-6����P'��m��2m-6������AP'=DP'ʱ����P��AD�Ĵ�ֱƽ�����ϣ�P'��1��-4������AD=AP'ʱ��16=��m+1��2+��2m-6��2��P'��![]() ��
��![]() ������AD=DP'ʱ��16=��m-3��2+��2m-6��2��P'��3+
������AD=DP'ʱ��16=��m-3��2+��2m-6��2��P'��3+![]() ��
��![]() ����P'��3-
����P'��3-![]() ��
��![]() �������ֱ��AP�Ľ���ʽ������ƽ�ƺ�P'���������ֱ��A'P'�Ľ���ʽ���ݴ����A'�����꼴�ɣ�
�������ֱ��AP�Ľ���ʽ������ƽ�ƺ�P'���������ֱ��A'P'�Ľ���ʽ���ݴ����A'�����꼴�ɣ�
��1��������ɵã�A��-1��0����B��0��1����
��C��0��-6����tan��OCD=![]() ��
��
��D��3��0����
��CD=3![]() ��
��
��FG=2![]() ��
��
��F'G'=2![]() ��
��
����D��DN��AB������F'��F'N��DG'������C����ֱ��AB�ĶԳƵ�G'������G'N��AB�Ľ���ΪF'��
��ʱG'D=F'N��G'F'=F'C��
���ı���CDG'F'�ܳ�=CD+F'G'+CF'+G'D=3![]() +2
+2![]() +F'G'+F'N=3
+F'G'+F'N=3![]() +2
+2![]() +G'N��
+G'N��
AB�Ľ���ʽΪy=x+1��
��DN��ֱ�߽���ʽΪy=x-3��
��ND=2![]() ��
��
��N��1��-2����
G'��-7��1����
��G'N=![]() ��
��
���ı���CDG'F'�ܳ�����СֵΪ3![]() +2
+2![]() +
+![]() ��
��
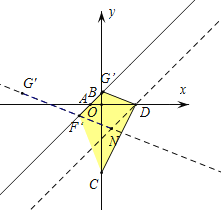
��2�����ڣ�
��ֱ��CD�Ľ���ʽΪ��![]() ��
��
����C��0��-6����D��3��0���ã�
![]() �� ��ã�
�� ��ã�![]()
��CD��ֱ�߽���ʽΪy=2x-6����P'��m��2m-6����
��AP��AB��
��AP����ֱ�߽���ʽΪy=-x-1��
��AP'=DP'ʱ����P��AD�Ĵ�ֱƽ�����ϣ�
��P'��1��-4����
��ֱ��A'P'��ֱ��APƽ�Ƶõ���
����ֱ��A'P'�Ľ���ʽΪ��y=-x+b1������P'��1��-4���ã�b1=-3
��A'P'��ֱ�߽���ʽΪy=-x-3��
����������![]() ����ã�
����ã�![]()
��A'��-2��-1����
��AD=AP'ʱ��16=��m+1��2+��2m-6��2��
��m=3��m=![]() ��
��
��P'��3��0�����ᣩ��P'��![]() ��
��![]() ����
����
ͬ�Ϸ����ɵã�
��A'P'��ֱ�߽���ʽΪy=-x-![]() ��
��
��A'��-![]() ��-
��-![]() ����
����
��AD=DP'ʱ��16=��m-3��2+��2m-6��2��
��m=3+![]() ��m=3-
��m=3-![]() ��
��
��P'��3+![]() ��
��![]() ����P'��3-
����P'��3-![]() ��-
��-![]() ����
����
ͬ�Ϸ����ɵã�
��AP'��ֱ�߽���ʽΪy=-x+3+![]() ��y=-x-3-
��y=-x-3-![]() ��
��
��A'��1+![]() ��2+
��2+![]() ����A'��-2-
����A'��-2-![]() ��-1-
��-1-![]() ����
����
��������A'��-2��-1����A'��-![]() ��-
��-![]() ����A'��1+
����A'��1+![]() ��2+
��2+![]() ����A'��-2-
����A'��-2-![]() ��-1-
��-1-![]() ����
����

 ��һ������Ԫͬ�����ؾ�ϵ�д�
��һ������Ԫͬ�����ؾ�ϵ�д�