题目内容
【题目】如图1, △ABC中,CD⊥AB于D,且BD: AD:CD=2:3:4,
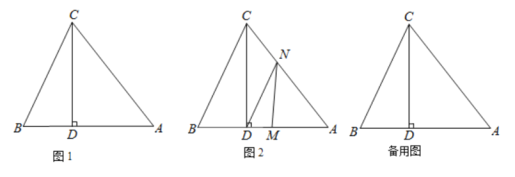
(1)试说明△ABC是等腰三角形;
(2)已知S△ABC=40cm2,如图2,动点M从点B出发以每秒1cm的速度沿线段BA向点A运动,同时动点N从点A出发以相同速度沿线段AC向点C运动,当其中一点到达终点时整个运动都停止.设点M运动的时间为t(秒),若△DMN的边与BC平行,求t的值;
【答案】(1)见解析(2)5或6.
【解析】
(1)设BD=2x,AD=3x,CD=4x,则AB=5x,由勾股定理求出AC,即可得出结论;
(2)由△ABC的面积求出BD、AD、CD、AC;当MN∥BC时,AM=AN;当DN∥BC时,AD=AN;得出方程,解方程即可.
(1)证明:设BD=2x,AD=3x,CD=4x,
则AB=5x,
在Rt△ACD中,AC=![]() =5x,
=5x,
∴AB=AC,
∴△ABC是等腰三角形;
(2)S△ABC=![]() ×5x×4x=40cm2,而x>0,
×5x×4x=40cm2,而x>0,
∴x=2cm,
则BD=4cm,AD=6cm,CD=8cm,AC=10cm.
①当MN∥BC时,AM=AN,
即10t=t,
∴t=5;
当DN∥BC时,AD=AN,
得:t=6;
∴若△DMN的边与BC平行时,t值为5或6.

 金牌课堂练系列答案
金牌课堂练系列答案 三新快车金牌周周练系列答案
三新快车金牌周周练系列答案【题目】小方家住户型呈长方形,平面图如下(单位:米),现准备铺设地面,三间卧室铺设木地板,其它区城铺设地砖.
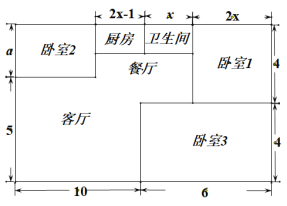
(1)求a的值.
(2)铺设地面需要木地板和地砖各多少平方米(用含![]() 的代数式表示)?
的代数式表示)?
(3)按市场价格,木地板单价为300元/平方米,地砖单价为100元/平方米,装修公司有![]() 两种活动方案,如表:
两种活动方案,如表:
活动方案 | 木地板价格 | 地砖价格 | 总安装费 |
A | 8折 | 8.5折 | 2000元 |
B | 9折 | 8.5折 | 免收 |
已知卧室2的面积是21平方米,则小方家应选择哪种活动,使铺设地面的总费用(包括材料费及安装费)更低?