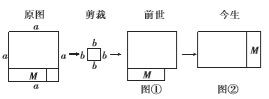
题目内容
【题目】已知关于x的一元二次方程ax2+bx+c=0(a≠0)有两个实数根x1,x2,请用配方法探索有实数根的条件,并推导出求根公式,证明x1x2=![]() .
.
【答案】证明见解析.
【解析】由a不为0,在方程两边同时除以a,把二次项系数化为1,然后把常数项移项到方程右边,两边都加上一次项系数一半的平方即(![]() )2,左边变为完全平方式,右边大于等于0时,开方即可得到求根公式;由求根公式求出的两个根相乘,化简后即可得证.
)2,左边变为完全平方式,右边大于等于0时,开方即可得到求根公式;由求根公式求出的两个根相乘,化简后即可得证.
∵ax2+bx+c=0(a≠0),
∴x2+![]() x=﹣
x=﹣![]() ,
,
∴x2+![]() x+(
x+(![]() )2=﹣
)2=﹣![]() +(
+(![]() )2,
)2,
即(x+![]() )2=
)2=![]() ,
,
∵4a2>0,
∴当b2﹣4ac≥0时,方程有实数根,
∴x+![]() =±
=±![]() ,
,
∴当b2﹣4ac>0时,x1=![]() ,x2=
,x2=![]() ;
;
当b2﹣4ac=0时,x1=x2=﹣![]() ;
;
∴x1x2=![]()
![]()
=![]()
=![]()
=![]()
=![]() ,
,
或x1x2=(﹣![]() )2=
)2=![]() =
=![]() =
=![]() ,
,
∴x1x2=![]() .
.

 名校课堂系列答案
名校课堂系列答案【题目】小方家住户型呈长方形,平面图如下(单位:米),现准备铺设地面,三间卧室铺设木地板,其它区城铺设地砖.
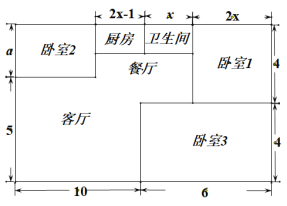
(1)求a的值.
(2)铺设地面需要木地板和地砖各多少平方米(用含![]() 的代数式表示)?
的代数式表示)?
(3)按市场价格,木地板单价为300元/平方米,地砖单价为100元/平方米,装修公司有![]() 两种活动方案,如表:
两种活动方案,如表:
活动方案 | 木地板价格 | 地砖价格 | 总安装费 |
A | 8折 | 8.5折 | 2000元 |
B | 9折 | 8.5折 | 免收 |
已知卧室2的面积是21平方米,则小方家应选择哪种活动,使铺设地面的总费用(包括材料费及安装费)更低?
【题目】某地试行医保制度,并规定:
一、每位居民年初缴纳医保基金70元;
二、居民个人当年看病的医疗费(以定点医院的医疗发票为准,年底按下表所示的方式结算)报销看病的医疗费用.
居民个人当年看病的医疗费用 | 医疗费用报销办法 |
不超过 n 元的部分 | 全部由医保基金承担(即全额报销) |
超过 n 元但不超过 6 000 元的部分 | 个人承担 |
超过 6 000 元的部分 | 个人承担 |
设一位居民当年看病的医疗费用为![]() 元,他个人实际承担的医疗费用(包括医疗费用中个人承担的部分和年初缴纳的医保基金)记为
元,他个人实际承担的医疗费用(包括医疗费用中个人承担的部分和年初缴纳的医保基金)记为![]() 元.
元.
(1)写出如下条件,![]() 的代数式(可含有
的代数式(可含有![]() ).
).
①当![]() 时;
时;
②当![]() 时.
时.
(2)已知![]() ,若该地居民周大爷某一年个人实际承担的医疗费用是
,若该地居民周大爷某一年个人实际承担的医疗费用是![]() 元,那么他这一年看病所花费的医疗费共多少元?
元,那么他这一年看病所花费的医疗费共多少元?