题目内容
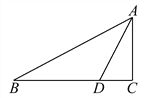
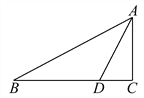
【题目】如图,已知在Rt△ABC中,∠C=90°,D是BC边上一点,AC=6,CD=3,∠ADC=α.
(1)试写出α的正弦、余弦、正切这三个函数值;
(2)若∠B与∠ADC互余,求BD及AB的长.
【答案】(1)sinα=![]() ,cosα=
,cosα=![]() ,tanα=2;(2)BD=9,AB=6
,tanα=2;(2)BD=9,AB=6![]() .
.
【解析】试题分析:(1)利用勾股定理求出AD的长度,再根据公式分别求出sinα、cosα、tanα的值;(2)由已知条件不难推出∠DAC=∠B,即tan∠DAC=tan∠B,算出tan∠DAC,即可算出BC、AD的长度,从而算出BD 的长度.
试题解析:
∵AC=6,CD=3,∴AD=![]() =3
=3![]() ,
,
∴sinα=![]() =
=![]() =
=![]() ,cosα=
,cosα=![]() =
=![]() =
=![]() ,tanα=
,tanα=![]() =
=![]() =2;
=2;
(2)∵∠C=90°,∴∠ADC+∠DAC=90°,
∵∠B+∠ADC=90°,∴∠DAC=∠B,
∵tan∠DAC=![]() =
=![]() =
=![]() ,∴tan∠B=
,∴tan∠B=![]() =
=![]() ,
,
∴BC=12,
∴BD=9,AB=![]() =6
=6![]() .
.

【题目】某烤鸭店在确定烤鸭的烤制时间时,主要依据的是下表的数据:
鸭的质量/千克 | 1 | 1.5 | 2 | 2.5 | 3 | 3.5 | 4 |
烤制时间/分 | 60 | 80 | 100 | 120 | 140 | 160 | 180 |
设鸭的质量为x千克,烤制时间为t,估计当x=2.9千克时,t的值为________________
【题目】广安某大型蔬菜超市从蔬菜批发市场批发蔬菜进行零售,部分蔬菜批发价格与零售价格如表:
蔬菜品种 | 西红柿 | 青椒 | 西兰花 | 豆角 |
批发价(元/ | 3.6 | 5.4 | 8 | 4.8 |
零售价(元/ | 5.4 | 8.4 | 14 | 7.6 |
请解答下列问题:
(1)第一天,该蔬菜超市批发青椒和豆角两种蔬菜共![]() ,用去了
,用去了![]() 元钱,问该蔬菜超市批发青椒和豆角两种蔬菜各多少千克?
元钱,问该蔬菜超市批发青椒和豆角两种蔬菜各多少千克?
(2)在(1)的条件,这两种蔬菜当天全部售完一共能盈利多少?
(3)第二天,蔬菜超市用![]() 元钱批发青椒和西兰花,要想当天全部售完后所盈利不少于
元钱批发青椒和西兰花,要想当天全部售完后所盈利不少于![]() 元,则该经营户最多能批发青椒多少?(结果取整数)
元,则该经营户最多能批发青椒多少?(结果取整数)