题目内容
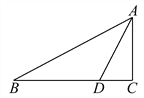
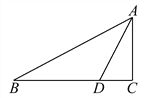
【题目】如图,已知在Rt△ABC中,∠C=90°,D是BC边上一点,AC=6,CD=3,∠ADC=α.
(1)试写出α的正弦、余弦、正切这三个函数值;
(2)若∠B与∠ADC互余,求BD及AB的长.
【答案】(1)sinα=![]() ,cosα=
,cosα=![]() ,tanα=2;(2)BD=9,AB=6
,tanα=2;(2)BD=9,AB=6![]() .
.
【解析】试题分析:(1)利用勾股定理求出AD的长度,再根据公式分别求出sinα、cosα、tanα的值;(2)由已知条件不难推出∠DAC=∠B,即tan∠DAC=tan∠B,算出tan∠DAC,即可算出BC、AD的长度,从而算出BD 的长度.
试题解析:
∵AC=6,CD=3,∴AD=![]() =3
=3![]() ,
,
∴sinα=![]() =
=![]() =
=![]() ,cosα=
,cosα=![]() =
=![]() =
=![]() ,tanα=
,tanα=![]() =
=![]() =2;
=2;
(2)∵∠C=90°,∴∠ADC+∠DAC=90°,
∵∠B+∠ADC=90°,∴∠DAC=∠B,
∵tan∠DAC=![]() =
=![]() =
=![]() ,∴tan∠B=
,∴tan∠B=![]() =
=![]() ,
,
∴BC=12,
∴BD=9,AB=![]() =6
=6![]() .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目