Question

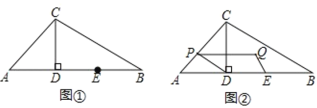
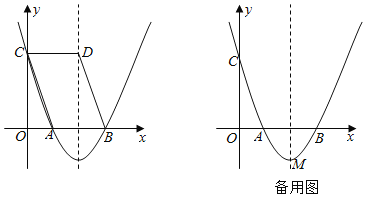
【题目】如图，已知二次函数y＝ax2﹣8ax+6（a＞0）的图象与x轴分别交于A、B两点，与y轴交于点C，点D在抛物线的对称轴上，且四边形ABDC为平行四边形．

（1）求此抛物线的对称轴，并确定此二次函数的表达式；

（2）点E为x轴下方抛物线上一点，若△ODE的面积为12，求点E的坐标；

（3）在（2）的条件下，设抛物线的顶点为M，点P是抛物线的对称轴上一动点，连接PE、EM，过点P作PE的垂线交抛物线于点Q，当∠PQE＝∠EMP时，求点Q到抛物线的对称轴的距离．

Answer 1

【答案】（1）x＝4，y＝x2﹣4x+6；（2）(3，-)；（3）4或2+

【解析】

（1）先求出对称轴为x＝4，进而求出AB＝4，进而求出点A，B坐标，即可得出结论；

（2）根据E点在抛物线y＝x2﹣4x+6上，设E（m，m2﹣4m+6），作EN⊥y轴于N，利用面积的和差：S梯形CDEN﹣S△OCD﹣S△OEN＝S△ODE建立方程求解，即可得出结论；

（3）①当点Q在对称轴右侧时，先判断出点E，M，Q，P四点共圆，得出∠EMQ＝90°，利用同角的余角相等判断出∠EMF＝∠HGM，得出tan∠EMF＝＝2，得出HG＝HM＝1，进而求出Q（8，6），得出结论；

②当点Q在对称轴左侧时，先判断出△PDQ∽△EFP，得出，进而判断出DP＝，PF＝2QD，即可得出结论．

解：（1）对称轴为直线x＝﹣，则CD＝4，

∵四边形ABDC为平行四边形，

∴DC∥AB，DC＝AB，

∴DC＝AB＝4，

∴A（2，0），B（6，0），

把点 A（2，0）代入得y＝ax2﹣8ax+12得4a﹣16a+6＝0，解得a＝，

∴二次函数解析式为y＝x2﹣4x+6；

（2）如图1，设E（m，m2﹣4m+6），其中2＜m＜6，作EN⊥y轴于N，

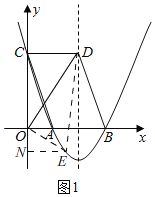
∵S梯形CDEN﹣S△OCD﹣S△OEN＝S△ODE，

∴（4+m）（6﹣m2+4m﹣6）﹣×4×6﹣m（﹣m2+4m﹣6）＝12，

化简得：m2﹣11m+24＝0，解得m1＝3，m2＝8（舍），

∴点E的坐标为（3，﹣）；

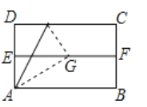
（3）①当点Q在对称轴右侧时，如图2，

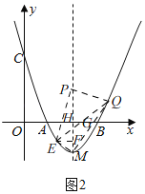
过点E作EF⊥PM于F，MQ交x轴于G，

∵∠PQE＝∠PME，

∴点E，M，Q，P四点共圆，

∵PE⊥PQ，

∴∠EPQ＝90°，

∴∠EMQ＝90°，

∴∠EMF+∠HMG＝90°，

∵∠HMG+∠HGM＝90°，

∴∠EMF＝∠HGM，

在Rt△EFM中，EF＝1，FM＝，tan∠EMF＝＝2，

∴tan∠HGM＝2，

∴，

∴HG＝HM＝1，

∴点G（5，0），

∵M（4，﹣2），

∴直线MG的解析式为y＝2x﹣10①，

∵二次函数解析式为y＝x2﹣4x+6②，

联立①②解得，（舍）或，

∴Q（8，6），

∴点Q到对称轴的距离为8﹣4＝4；

②当点Q在对称轴左侧时，如图3，

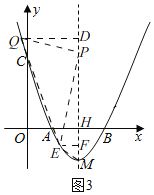
过点E作EF⊥PM于F，过点Q作QD⊥PM于D，

∴∠DQP+∠QPD＝90°，

∵∠EPQ＝90°，

∴∠DPQ+∠FPE＝90°，

∴∠DQP＝∠FPE，

∵∠PDQ＝∠EFP，

∴△PDQ∽△EFP，

∴，

由①知，tan∠PQE＝＝2，

∵EF＝1，

∴＝，

∴DP＝，PF＝2QD，

设Q（n，n2﹣4n+6），

∴DQ＝4﹣n，DH＝n2﹣4n+6，

∴PF＝DH+FH﹣DP＝n2﹣4n+6+﹣＝n2﹣4n+7，

∴n2﹣4n+7＝2（4﹣n），

∴n＝2+（舍）或n＝2﹣，

∴DQ＝4﹣n＝2+，

即点Q到对称轴的距离为4或2+．