Question

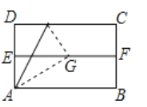
【题目】如图，对折矩形纸片ABCD，使AB与DC重合得到折痕EF，将纸片展平，再一次折叠，使点D落到EF上点G处，并使折痕经过点A，已知BC＝2，则线段EG的长度为________．

Answer 1

【答案】

【解析】

直接利用翻折变换的性质以及直角三角形的性质得出∠2=∠4，再利用平行线的性质得出∠1=∠2=∠3，进而得出答案．

解：如答图，由第一次折叠得EF⊥AD，AE＝DE，

∴∠AEF＝90°，AD＝2AE．

∵四边形ABCD是矩形，

∴∠D＝∠DAB＝90°，

∴∠AEF＝∠D，

∴EF∥CD，

∴△AEN∽△ADM，

∴＝＝，

∴AN＝AM，

∴AN＝MN，

又由第二次折叠得∠AGM＝∠D＝90°，

∴NG＝AM，

∴AN＝NG，

∴∠2＝∠4．

由第二次折叠得∠1＝∠2，

∴∠1＝∠4．

∵AB∥CD，EF∥CD，

∴EF∥AB，∴∠3＝∠4，

∴∠1＝∠2＝∠3．

∵∠1＋∠2＋∠3＝∠DAB＝90°，

∴∠1＝∠2＝∠3＝30°．

∵四边形ABCD是矩形，

∴AD＝BC＝2．

由第二次折叠得AG＝AD＝2．

由第一次折叠得AE＝AD＝×2＝1．

在Rt△AEG中，由勾股定理得EG＝＝＝，

故答案为：．