题目内容
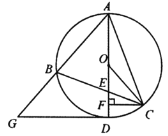
【题目】如图①,在△ABC 中,CD⊥AB 于点 D,AD=CD=2,BD=4,点 E 是线段BD 的中点,点 P 从点 A 出发,沿折线 AC-CB 向终点 B 运动,点 P 在边 AC 上的速度为每秒![]() 个单位长度,P在BC边上的速度为
个单位长度,P在BC边上的速度为![]() 个单位长度,设P的运动时间为 t(秒).
个单位长度,设P的运动时间为 t(秒).
(1)用含 t 的代数式表示点 P 到直线 AB 的距离.
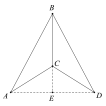
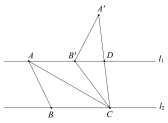
(2)如图②,作点 P 关于直线 CD 的对称点 Q,设以 D、E、Q、P 为顶点的四边形的面积为 S(平方单位),求 S 与 t 之间的函数关系式.
(3)当点 P 在边 BC 上时,在△BCD 的边上(不包括顶点)存在点 H,使四边形 DEPH为轴对称图形,直接写出此时线段 CP 的长.
【答案】(1)![]() 或
或![]() ;(2)
;(2)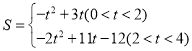 ;(3)
;(3)![]() 或
或![]() 或
或![]() 或
或![]()
【解析】
(1)分两种情况:
①当P在边AC上时,如图1,根据△APG是等腰直角三角形,可得![]() ;
;
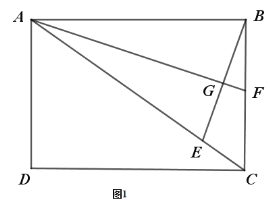
②当P在边BC上时,如图2,根据三角函数sin∠B,可得PG的长;
(2)分两种情况:
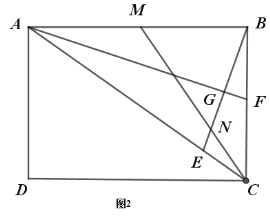
①当0<t<2时,P在边AC上,如图3,②当2<t<4时,P在边BC上,如图4,
四边形PQDE是梯形,根据梯形面积公式代入可得结论;
(3)分4种情况:
①如图5,当四边形DEPH是矩形时;②如图6,当四边形DEPH是等腰梯形时;③如图7,过D作DP⊥BC于P,过E作EH⊥PD,交CD于H,④如图8,过E作EP⊥BC于P,在BC上取点H,使PH=EP,连接DH,③和④是筝形;分别求出各情况的CP的长即可.
(1)过P作PG⊥AB于G,
分两种情况:
①当P在边AC上时,如图1,
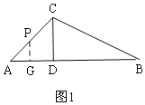
Rt△ADC中,AD=CD=2,
∴∠A=45°,
∴△APG是等腰直角三角形,
由勾股定理得:AC=![]() ,
,
P走完AC段所花时间为:![]() (秒),
(秒),
P在边AC上,即0![]() 2时,
2时,
由题意得:AP=![]() ,
,
∴AG=PG= AP![]() =
=![]() ,
,
即点P到直线AB的距离是t;
②当P在边BC上时,如图2,
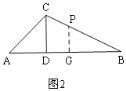
BC=![]() ,
,
P走完BC段所花时间为:![]() ,
,
P在边BC上,即2![]() 4时,
4时,
由题意得:CP=![]() ,
,
∴BP= BC - CP =![]() ,
,
sin∠B=![]() ,
,
∴![]() ,
,
∴PG=![]() ,
,
即点P到直线AB的距离是![]() ;
;
(2)分两种情况:
①当0<t<2时,P在边AC上,如图3,
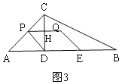
设PQ与CD交于H,
∵点P关于直线CD的对称点Q,
∴PQ⊥CD,
∵AB⊥CD,
∴PQ∥AB,
∴△CPH∽△CAD,
∴![]() ,
,
∴![]() ,
,
∴PH=CH=![]() ,PQ=2PH=
,PQ=2PH=![]() ,
,
∵BD=4,点 E 是线段BD 的中点,
∴DE=![]() ,
,
∴DH=CD-CH ![]() ,
,
∴![]() ;
;
②当2<t<4时,P在边BC上,如图4,
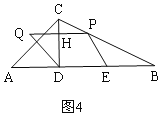
设PQ与CD交于H,
由题意得:CP![]() ,
,
同理PQ∥AB,
∴△CPH∽△CBD,
∴![]() ,
,
∴![]() ,
,
∴PH=2(![]() ),CH=
),CH=![]() ,
,
∴DH=CD-CH=2![]() (
(![]() )=
)=![]() ,PQ=2PH=4
,PQ=2PH=4![]() )=
)=![]() ,
,
∴![]() ;
;
(3)分4种情况:
①如图5,
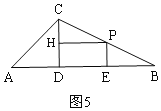
当四边形DEPH是矩形时,四边形DEPH是轴对称图形,
∴PE∥CD,
∵点 E 是线段BD 的中点,
∴P是BC的中点,
∴CP=![]() ;
;
②如图6,
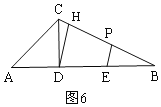
当四边形DEPH是等腰梯形时,四边形DEPH是轴对称图形,
∴DH∥PE,
则BD=BH=4,BE=PB=2,
此时CP![]() ;
;
③如图7,
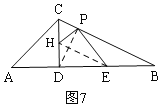
过D作DP⊥BC于P,过E作EH⊥PD,交CD于H,
∴EH∥BC,
∵E是BD的中点,
∴EH是PD的中垂线,
∴PH=DH,PE=DE,
∴四边形DEPH为轴对称图形,![]() =
=![]() ,
,
∴![]() ,
,
∴![]() ,
,
由勾股定理得:CP=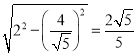 ;
;
④如图8,
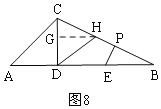
过E作EP⊥BC于P,在BC上取点H,使PH=EP,连接DH,过H作HG⊥CD于G,
∵Rt△EPB![]() Rt△CDB中,BE=2,
Rt△CDB中,BE=2,
∴![]() ,
,
∴![]() ,
,
∴EP=![]() ,PB=
,PB=![]() ,
,
CH=BC-PH-PB=![]() ,
,
∵GH∥BD,
∴△CGH∽△CDB,
∴![]() ,
,
∴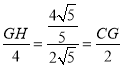 ,
,
∴![]() ,
,![]() ,
,
∴![]() ,
,
由勾股定理得: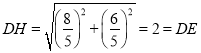 ,
,
∴四边形DEPH为轴对称图形,
此时CP=CH+HP=![]() ;
;
综上所述,CP的长为:![]() 或
或![]() 或
或![]() 或
或![]() .
.

 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案