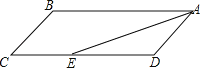
题目内容
【题目】在![]() 中,
中,![]() ,点D是
,点D是![]() 外一点,点D与点C在直线
外一点,点D与点C在直线![]() 的异侧,且点
的异侧,且点![]() 不共线,连接
不共线,连接![]() .
.


(1)如图1,当![]() 时,画出图形,直接写出
时,画出图形,直接写出![]() 之间的数量关系;
之间的数量关系;
(2)当![]() 时,利用图2,继续探究
时,利用图2,继续探究![]() 之间的数量关系并证明;
之间的数量关系并证明;
(提示:尝试运用图形变换,将要研究的有关线段尽可能转移到一个三角形中)
(3)当![]() 时,进一步探究
时,进一步探究![]() 之间的数量关系,并用含
之间的数量关系,并用含![]() 的等式直接表示出它们之间的关系.
的等式直接表示出它们之间的关系.
【答案】(1)图形见解析,![]() 之间的数量关系是
之间的数量关系是![]() ;(2)
;(2)![]() ;(3)
;(3)![]()
【解析】
(1)画出图形即可证得△ABC是等边三角形,以BD为边向外作等边△BDE,利用SAS可证明△ABE≌△CBD故AE=CD,运用勾股定理即可的出答案;
(2)过点A作![]() ,且
,且![]() ,利用勾股定理可得
,利用勾股定理可得![]() ,利用SAS可证明
,利用SAS可证明![]() ,可得
,可得![]() .
.
运用勾股定理在![]() 中,
中,![]() ,即可得出答案;
,即可得出答案;
(3)以BD为底边构造等腰△BDE,使![]() ,连接AE,CD,过点A作AH⊥BC于点H,由两边成比例和它们的夹角相等可判定△ABC∽△EBD,故∠ABC=∠ACB=∠EBD=∠EDB
,连接AE,CD,过点A作AH⊥BC于点H,由两边成比例和它们的夹角相等可判定△ABC∽△EBD,故∠ABC=∠ACB=∠EBD=∠EDB![]() ,可得∠ADE=90°.
,可得∠ADE=90°.
由△BED∽△BAC可得:![]() ,进而证明△EBA∽△DBC,可得
,进而证明△EBA∽△DBC,可得![]() 有三角函数可得
有三角函数可得![]() 推出
推出 ,
,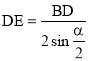 ,利用勾股定理,将AE、DE代入
,利用勾股定理,将AE、DE代入![]() 即可得出答案
即可得出答案
解:(1)
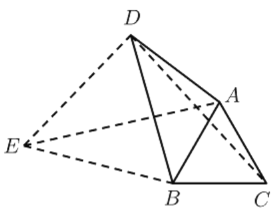
∵![]() ,AB=AC
,AB=AC
∴∠ABC=∠ACB=∠BAC=60°
∴△ABC是等边三角形
以BD为边向外作等边△BDE连接AE,CD
∵△ABC,△BDE都是等边三角形
∴BA=BC=AC,BD=BE=DE
∠ABC=∠DBE=60°
∴∠ABC+∠ABD=∠DBE+∠ABD
∴∠CBD=∠ABE
在△ABE和△CBD中
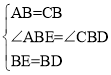
∴△ABE≌△CBD(SAS)
∴AE=CD
∵∠ADB=30°,∠BDE=60°
∴∠ADE=∠ADB+∠BDE=90°
在Rt△ADE中![]()
即![]()
故答案为:![]()
(2)如图,过点A作![]() ,且
,且![]() ,连接
,连接![]() .
.
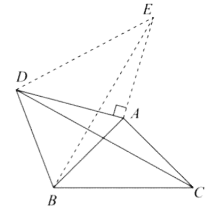
![]() .
.
可得![]() .
.
![]() ,
,
![]() .
.
又![]() ,
,
![]()
![]() .
.
在![]() 中,
中,![]() .
.
![]() .
.
(3)以BD为底边构造等腰△BDE
使![]() ,连接AE,CD
,连接AE,CD
过点A作AH⊥BC于点H
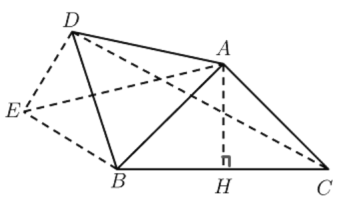
∵AB=AC,BE=DE,∠BAC=∠BED=![]()
∴![]()
∴△ABC∽△EBD
∴∠ABC=∠ACB=∠EBD=∠EDB
=![]()
=![]()
∵![]()
∴∠ADE=∠ADB+∠EDB=90°
∵△BED∽△BAC
∴![]()
∵∠EBD+∠ABD=∠ABC+∠ABD
∴∠EBA=∠DBC
∴![]()
∴△EBA∽△DBC
∴![]()
∴AB=AC,AH⊥BC
∴![]()
∴![]()
∴![]()
∴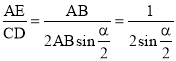
∴
同理![]()
∴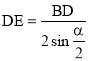
在Rt△ADE中![]()
∴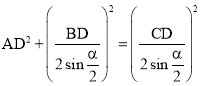
∴![]()
即![]() .
.
故答案为:![]()

 期末100分闯关海淀考王系列答案
期末100分闯关海淀考王系列答案【题目】下面是“作一个![]() 角”的尺规作图过程.
角”的尺规作图过程.
已知:平面内一点A. 求作: |
作法:如图,
①作射线 ②在射线 ③分别以 ④作射线 则 |
(1)使用直尺和圆规,补全图形;(保留作图痕迹)
(2)完成下面的证明.
证明:![]() ,
,
![]() ______
______![]() _______
_______![]() .
.
![]() _____
_____![]() .(_____________)(填推理的依据)
.(_____________)(填推理的依据)