Question

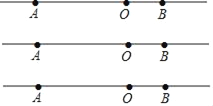
【题目】如图，A，B分别是数轴上两点，点O为原点，点A表示的数为﹣60，点B表示的数为30．现有两个动点P、Q均从点A出发，沿数轴正方向移动，点P的速度为6单位/秒，点Q的速度为3单位/秒．

（1）若两动点同时出发，当点P到达点B时，点Q在数轴上表示的数为_____；

（2）若点P出发2秒钟后点Q出发，当点P到达点B时，P、Q两点同时停止运动，设点P运动的时间为t秒，运动过程中点P表示的数为x，点Q表示的数为y，求t为何值时，|y|=2|x|．

（3）在（1）的条件下，若点P到达点B停留5秒后以5单位/秒的速度匀速沿数轴向点A运动，求在整个运动过程中当t为何值时，P，Q两点相距20个单位长度．

Answer 1

【答案】(1)-15;(2) 当t=6或秒时，|y|=2|x|;(3) 在整个运动过程中当t为、或秒时，P，Q两点相距20个单位长度

【解析】

（1）根据点A、B表示的数可得出线段AB的长度，利用时间=路程÷速度可求出当点P到达点B时点P、Q运动的时间，再由点Q的出发点、速度及运动时间可得出当点P到达点B时点Q在数轴上表示的数；
（2）找出当运动时间为t秒时x、y的值，结合|y|=2|x|即可得出关于t的含绝对值符号的一元一次方程，解之即可得出结论；
（3）分析整个运动过程，由点P的运动速度不同可分三段考虑：当0≤t≤15时，找出点P、Q表示的数，由线段PQ=20可得出关于t的一元一次方程，解之即可得出t值；当15<t≤20时，找出点P、Q表示的数，由线段PQ=20可得出关于t的一元一次方程，解之即可得出t值；当t>20时，找出点P、Q表示的数，由线段PQ=20可得出关于t的一元一次方程，解之即可得出t值．综上即可得出结论．

解：（1）∵点A表示的数为﹣60，点B表示的数为30，

∴线段AB的长度为30﹣（﹣60）=90，

∴当点P到达点B时，点P、Q运动的时间为90÷6=15（秒），

∴当点P到达点B时，点Q在数轴上表示的数为﹣60+3×15=﹣15．

故答案为：﹣15．

（2）当点P运动的时间为t秒时，x=6t﹣60，y=3（t﹣2）﹣60=3t﹣66．

∵|y|=2|x|，即|3t﹣66|=2|6t﹣60|，

解得：t1=6，t2=．

答：当t=6或秒时，|y|=2|x|．

（3）∵90÷6=15（秒），15+5=20（秒），

∴分三种情况考虑：

①当0≤t≤15时，点P表示的数为6t﹣60，点Q表示的数为3t﹣60，

∴6t﹣60﹣（3t﹣60）=20，

解得：t=

②当15＜x≤20时，点P表示的数为30，点Q表示的数为3t﹣60，

∴30﹣（3t﹣60）=20，

解得：t=（不合题意，舍去）；

当t＞20时，点P表示的数为30﹣5（t﹣20），点Q表示的数为3t﹣60，

∴|30﹣5（t﹣20）﹣（3t﹣60）|=20，

解得：t1=，t2=．

综上所述：在整个运动过程中当t为、或秒时，P，Q两点相距20个单位长度．