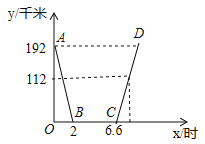
题目内容
【题目】如图,AB是⊙O的一条弦,且AB= ![]() .点C,E分别在⊙O上,且OC⊥AB于点D,∠E=30°,连接OA.
.点C,E分别在⊙O上,且OC⊥AB于点D,∠E=30°,连接OA. 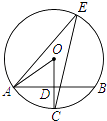
(1)求OA的长;
(2)若AF是⊙O的另一条弦,且点O到AF的距离为 ![]() ,直接写出∠BAF的度数.
,直接写出∠BAF的度数.
【答案】
(1)解:∵OC⊥AB,AB= ![]() ,
,
∴AD=DB=2 ![]() ,
,
∵∠E=30°,
∴∠AOD=60°,∠OAB=30°,
∴OA= ![]() =4
=4
(2)解:如图,作OH⊥AF于H,
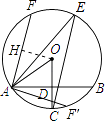
∵OA=4,OH=2 ![]() ,
,
∴∠OAF=45°,
∴∠BAF=∠OAF+∠OAB=75°,
则∠BAF′=∠OAF′﹣∠OAB=15°,
∴∠BAF的度数是75°或15°.
【解析】(1)根据垂径定理求出AD的长,根据圆周角定理求出∠AOD的度数,运用正弦的定义解答即可;(2)作OH⊥AF于H,根据勾股定理和等腰直角三角形的性质求出∠OAF的度数,分情况计算即可.
【考点精析】解答此题的关键在于理解勾股定理的概念的相关知识,掌握直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2,以及对垂径定理的理解,了解垂径定理:平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧.

练习册系列答案
 名校通行证有效作业系列答案
名校通行证有效作业系列答案
相关题目