ЬтФПФкШн
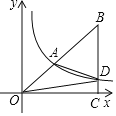
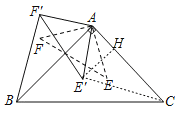
ЁОЬтФПЁПШчЭМ1ЃЌдкЁїABCжаЃЌЁЯBACЃН90ЁуЃЌABЃНACЃЌDЮЊБпABЩЯвЛЕуЃЌСЌНгCDЃЌдкЯпЖЮCDЩЯШЁвЛЕуEЃЌвдAEЮЊжБНЧБпзїЕШбќжБНЧЁїAEFЃЌЪЙЁЯEAFЃН90ЁуЃЌСЌНгBFНЛCDЕФбгГЄЯпгкЕуPЃЎ

ЃЈ1ЃЉЬНЫїЃКCEгыBFгаКЮЪ§СПЙиЯЕКЭЮЛжУЙиЯЕЃПВЂЫЕУїРэгЩЃЛ
ЃЈ2ЃЉШчЭМ2ЃЌШєABЃН2ЃЌAEЃН1ЃЌАбЁїAEFШЦЕуAЫГЪБеыа§зЊжСЁїAE'FЁфЃЌЕБЁЯEЁфACЃН60ЁуЪБЃЌЧѓBFЁфЕФГЄЃЎ
ЁОД№АИЁПЃЈ1ЃЉCEЃНBFЃЌCEЁЭBFЃЌРэгЩМћНтЮіЃЛЃЈ2ЃЉ![]()
ЁОНтЮіЁП
ЃЈ1ЃЉгЩЁАSASЁБПЩжЄЁїAECЁеЁїAFBЃЌПЩЕУCEЃНBFЃЌЁЯABFЃНЁЯACEЃЌНјЖјПЩЕУCEЁЭBFЃЛ
ЃЈ2ЃЉЙ§ЕуE'зїE'HЁЭACЃЌСЌНгE'CЃЌгЩжБНЧШ§НЧаЮЕФаджЪКЭЙДЙЩЖЈРэПЩЧѓE'CЕФГЄЃЌгЩЁАSASЁБПЩжЄЁїF'ABЁеЁїE'ACЃЌПЩЕУBF'ЃНCE'ЃН![]() ЃЎ
ЃЎ
ЃЈ1ЃЉCEЃНBFЃЌCEЁЭBFЃЌРэгЩШчЯТЃК
ЁпЁЯBACЃНЁЯEAFЃН90ЁуЃЌ
ЁрЁЯEACЃНЁЯFABЃЌ
гжЁпAEЃНAFЃЌABЃНACЃЌ
ЁрЁїAECЁеЁїAFBЃЈSASЃЉ
ЁрCEЃНBFЃЌЁЯABFЃНЁЯACEЃЌ
ЁпЁЯADCЃНЁЯBDPЃЌ
ЁрЁЯBPDЃНЁЯCADЃН90ЁуЃЌ
ЁрCEЁЭBFЃЛ
ЃЈ2ЃЉЙ§ЕуE'зїE'HЁЭACЃЌСЌНгE'CЃЌ
ЁпАбЁїAEFШЦЕуAЫГЪБеыа§зЊжСЁїAE'FЁфЃЌ
ЁрAFЃНAEЃНAE'ЃНAF'ЃН1ЃЌЁЯBAF'ЃНЁЯE'ACЃН60ЁуЃЌ
ЁпЁЯE'ACЃН60ЁуЃЌЁЯAHE'ЃН90ЁуЃЌ
ЁрЁЯAE'HЃН30ЁуЃЌ
ЁрAHЃН![]() AE'ЃН
AE'ЃН![]() ЃЌE'HЃН
ЃЌE'HЃН![]() AHЃН
AHЃН![]() ЃЌ
ЃЌ
ЁрHCЃНACЉAHЃН![]() ЃЌ
ЃЌ
ЁрE'CЃН![]() ЃН
ЃН![]() ЃЌ
ЃЌ
ЁпAF'ЃНAE'ЃЌЁЯF'ABЃНЁЯE'ACЃН60ЁуЃЌABЃНACЃЌ
ЁрЁїF'ABЁеЁїE'ACЃЈSASЃЉ
ЁрBF'ЃНCE'ЃН![]() ЃЎ
ЃЎ

 ЬьЬьЯђЩЯвЛБОКУОэЯЕСаД№АИ
ЬьЬьЯђЩЯвЛБОКУОэЯЕСаД№АИ аЁбЇЩњ10ЗжжггІгУЬтЯЕСаД№АИ
аЁбЇЩњ10ЗжжггІгУЬтЯЕСаД№АИЁОЬтФПЁПФГЩЬЕъЙКНјСЫвЛжжаТПюаЁЕчЦїЃЌЮЊСЫбАевКЯЪЪЕФЯњЪлМлИёЃЌНјааСЫЮЊЦк5жмЕФЪдгЊЯњЃЌЪдгЊЯњЕФЧщПіШчБэЫљЪОЃК
Ек1жм | Ек2жм | Ек3жм | Ек4жм | Ек5жм | |
ЪлМл/ЃЈдЊ/ЬЈЃЉ | 50 | 40 | 60 | 55 | 45 |
ЯњЪл/ЬЈ | 360 | 420 | 300 | 330 | 390 |
вбжЊИУПюаЁЕчЦїЕФНјМлУПЬЈ30дЊЃЌЩшИУПюаЁЕчЦїУПЬЈЕФЪлМлЮЊxдЊЃЌУПжмЕФЯњСПЮЊyЬЈЃЎ
ЃЈ1ЃЉЙлВьБэжаЕФЪ§ОнЃЌЭЦЖЯyгыxТњзуЪВУДКЏЪ§ЙиЯЕЃЌВЂЧѓГіетИіКЏЪ§ЙиЯЕЪНЃЛ
ЃЈ2ЃЉШєЯыУПжмЕФРћШѓЮЊ9000дЊЃЌдђЦфЪлМлгІЖЈЮЊЖрЩйдЊЃП
ЃЈ3ЃЉШєУПЬЈаЁЕчЦїЕФЪлМлВЛЕЭгк40дЊЃЌЕЋгжВЛФмИпгкНјМлЕФ2БЖЃЌдђШчКЮЖЈМлВХФмИќПьЕиМѕЩйПтДцЃПДЫЪБУПжмзюЖрПЩЯњЪлЖрЩйЬЈЃП