题目内容
【题目】如图为某城市部分街道示意图,四边形ABCD为正方形,点G在对角线BD上,GE⊥CD,GF⊥BC,AD=1 500 m,小敏行走的路线为B→A→G→E,小聪行走的路线为B→A→D→E→F.若小敏行走的路程为3 100 m,则AG+GE=______m,由此可得小聪行走的路程为_______m.

【答案】1600 4600
【解析】
连接GC,根据正方形的性质易证DE=GE,再证明△AGD≌△GDC,根据全等三角形的性质可得AG=CG;在矩形GECF中,根据矩形的对角线相等可得EF=CG,即可得EF=AG.根据小敏走的路程为BA+AG+GE=3100m,即可求得AG+GE的值;根据小聪行走的路程为BA+AD+DE+EF= BA+AD+ GE+AG,即可求得小聪所走的路程.
连接GC,
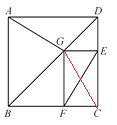
∵四边形ABCD为正方形,
∴AD=AB=CD=1500m,∠ADB=∠CDB=45°,
∵∠CDB=45°,GE⊥DC,
∴△DEG是等腰直角三角形,
∴DE=GE.
在△AGD和△GDC中,
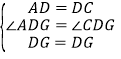
∴△AGD≌△GDC
∴AG=CG
在矩形GECF中,EF=CG,
∴EF=AG.
∵小敏共走了3100m,
∴BA+AG+GE=3100m,
∵AB=1500m,
∴AG+GE=1600m;
∴小聪行走的路程为:BA+AD+DE+EF= BA+AD+ GE+AG=1500+1500+1600=4600(m).
故答案为:1600;4600.

练习册系列答案
相关题目