��Ŀ����
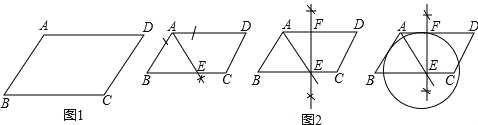
����Ŀ����ͼ,��һ�����Ͼ���ģ��ABCD����Ϊ10cm����Ϊ4cm�����������㹻���ֱ�����ǰ� PHF ��ֱ�Ƕ���P����AD����(����A��D�غ�)����AD���ʵ��ƶ����ǰ嶥��P:
���ܷ�ʹ������ǰ���ֱ�DZ߷ֱ�ͨ����B���C?���������������ʱ AP �ij�������������˵��������
���ٴ��ƶ����ǰ�λ����ʹ���ǰ嶥��P��AD���ƶ���ֱ�DZ�PH ʼ��ͨ����B����һֱ�DZ�PF��DC���ӳ��߽��ڵ�Q����BC���ڵ�E���ܷ�ʹCE=2cm?���������������ʱAP�ij���������������˵������.
���𰸡�������AP=8��2��������AP=4
��������
�������������AP=x�������ݾ��ε����ʣ���Rt��ABC��Rt��PDC��Rt��PBC���ֱ����ù��ɶ���������ý����
��������������������
����AP=x��������BP2=16+x2��CP2=16+(10-x)2��
����Rt��PBC������BP2+ CP2=BC2����16+x2+16+(10-x)2=100��
����x2-10x+16=0,��(x-5)2=9������x-5=��3������x=8��x=2����AP=8��2��
����.�����������AP=4.

��ϰ��ϵ�д�
�����Ŀ