题目内容
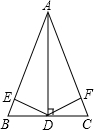
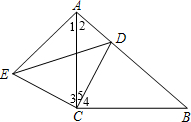
已知：如图，Rt△ABC中，∠ACB=90°，AC=BC，点D为AB边上一点，且不与A、B两
点重合，AE⊥AB，AE=BD，连接DE、DC．
（1）求证：△ACE≌△BCD；
（2）猜想：△DCE是______三角形；并说明理由．
点重合，AE⊥AB，AE=BD，连接DE、DC．（1）求证：△ACE≌△BCD；
（2）猜想：△DCE是______三角形；并说明理由．
（1）证明：
∵∠ACB=90°，AC=BC，
∴∠B=∠2=45°．
∵AE⊥AB，
∴∠1+∠2=90°．
∴∠1=45°．
∴∠1=∠B．
在△ACE和△BCD中，
∵
∴△ACE≌△BCD（SAS）．
（2）猜想：△DCE是等腰直角三角形；
理由说明：
∵△ACE≌△BCD，
∴CE=CD，∠3=∠4．
∵∠4+∠5=90°，
∴∠3+∠5=90°．
即∠ECD=90°．
∴△DCE是等腰直角三角形．
∵∠ACB=90°，AC=BC，
∴∠B=∠2=45°．
∵AE⊥AB，
∴∠1+∠2=90°．
∴∠1=45°．
∴∠1=∠B．
在△ACE和△BCD中，
∵
|
∴△ACE≌△BCD（SAS）．
（2）猜想：△DCE是等腰直角三角形；
理由说明：
∵△ACE≌△BCD，
∴CE=CD，∠3=∠4．
∵∠4+∠5=90°，
∴∠3+∠5=90°．
即∠ECD=90°．
∴△DCE是等腰直角三角形．
练习册系列答案
相关题目
下列说法中正确的个数是（ ）
①两腰对应相等的两个等腰三角形全等．②面积相等的两个等腰三角形全等．
③能够完全重合的两个三角形全等．④两个锐角对应相等的两个直角三角形全等．
①两腰对应相等的两个等腰三角形全等．②面积相等的两个等腰三角形全等．
③能够完全重合的两个三角形全等．④两个锐角对应相等的两个直角三角形全等．
| A．1个 | B．2个 | C．3个 | D．0个 |
