题目内容
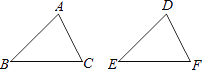
【题目】如图,![]() 和
和![]() 都是等腰直角三角形,
都是等腰直角三角形,![]() 交
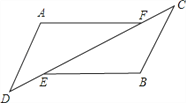
交![]() 于点
于点![]() 分别交
分别交![]() 于点
于点![]()
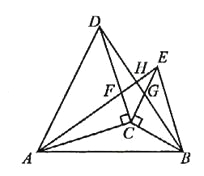
试猜测线段![]() 和
和![]() 的数量和位置关系,并说明理由.
的数量和位置关系,并说明理由.
【答案】![]()
【解析】
由于条件可知CD=AC,BC=CE,且可求得∠ACE=∠DCB,所以△ACE≌△DCB,即AE=BD,∠CAE=∠CDB;又因为对顶角相等即∠AFC=∠DFH,所以∠DHF=∠ACD=90°,即AE⊥BD.
猜测:![]()
理由如下:
∵∠ACD=∠BCE=90°,
∴∠ACD+∠DCE=∠BCE+∠DCE,
即∠ACE=∠DCB,
又∵△ACD和△BCE都是等腰直角三角形,
∴AC=CD,CE=CB,
在△ACE与△DCB中,
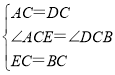
∴△ACE≌△DCB(SAS),
∴AE=BD,∠CAE=∠CDB;
∵∠AFC=∠DFH,∠FAC+∠AFC=90°,
∴∠DHF=∠ACD=90°,
∴AE⊥BD.
故线段AE和BD的数量相等,位置是垂直关系.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
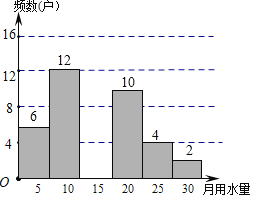
【题目】某校七(1)班学生为了解某小区家庭月均用水情况,随机调查了该小区部分家庭,并将调查数据进行如下整理,请解答以下问题;
级别 | A | B | C | D | E | F |
月均用水量x(t) | 0<x≤5 | 5<x≤10 | 10<x≤15 | 15<x≤20 | 20<x≤25 | 25<x≤30 |
频数(户) | 6 | 12 | m | 10 | 4 | 2 |
(1)本次调查采用的方式是 (填“全面调查”或“抽样调查);
(2)若将月均用水量的频数绘成形统计图,月均用水量“15<x≤20”组对应的圆心角度数是72°,则本次调查的样本容量是 ,表格中m的值是 ,补全频数分布直方图.
(3)该小区有500户家庭,求该小区月均用水量超过15t的家庭大约有多少户?