题目内容
【题目】四边形ABCD内接于⊙O,连接AC、BD,2∠BDC+∠ADB=180°.
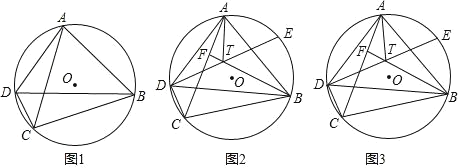
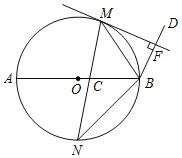
(1)如图1,求证:AC=BC;
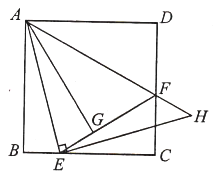
(2)如图2,E为⊙O上一点,![]() =
=![]() ,F为AC上一点,DE与BF相交于点T,连接AT,若∠BFC=∠BDC+
,F为AC上一点,DE与BF相交于点T,连接AT,若∠BFC=∠BDC+![]() ∠ABD,求证:AT平分∠DAB;
∠ABD,求证:AT平分∠DAB;
(3)在(2)的条件下,DT=TE,AD=8,BD=12,求DE的长.
【答案】(1)见解析;(2)见解析;(3)8![]()
【解析】
(1)只要证明∠CAB=∠CBA即可.
(2)如图2中,作TH⊥AD于H,TR⊥BD于R,TL⊥AB于L.想办法证明TL=TH即可解决问题.
(3)如图3中,连接EA,EB,作EG⊥AB,TH⊥AD于H,TR⊥BD于R,TL⊥AB于L,AQ⊥BD于Q.证明△EAG≌△TDH(AAS),推出AG=DH,证明Rt△TDR≌Rt△TDH(HL),推出DH=DR,同理可得AL=AH,BR=BL,设DH=x,则AB=2x,
由S△ADB=![]() BDAQ=
BDAQ=![]() ADh+
ADh+![]() ABh+
ABh+![]() DBh,可得AQ=
DBh,可得AQ=![]() h,再根据sin∠BDE=sin∠ADE,sin∠AED=sin∠ABD,构建方程组求出m即可解决问题.
h,再根据sin∠BDE=sin∠ADE,sin∠AED=sin∠ABD,构建方程组求出m即可解决问题.
解:(1)如图1中,
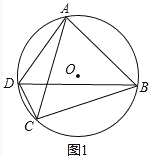
∵四边形ABCD内接于⊙O,
∴∠ADC+∠ABC=180°,
即∠ADB+∠BDC+∠ABC=180°,
∵2∠BDC+∠ADB=180°,
∴∠ABC=∠BDC,
∵∠BAC=∠BDC,
∴∠BAC=∠ABC,
∴AC=BC.
(2)如图2中,作TH⊥AD于H,TR⊥BD于R,TL⊥AB于L.
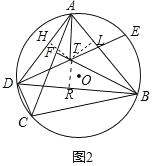
∵∠BFC=∠BAC+∠ABF,∠BAC=∠BDC,
∴∠BFC=∠BDC+∠ABF,
∵∠BFC=∠BDC+![]() ∠ABD,
∠ABD,
∴∠ABF=![]() ∠ABD,
∠ABD,
∴BT平分∠ABD,
∵![]() =
=![]()
∴∠ADE=∠BDE,
∴DT平分∠ADB,
∵TH⊥AD于H,TR⊥BD于R,TL⊥AB于L.
∴TR=TL,TR=TH,
∴TL=TH,
∴AT平分∠DAB.
(3)如3中,连接EA,EB,作EG⊥AB,TH⊥AD于H,TR⊥BD于R,TL⊥AB于L,AQ⊥BD于Q.
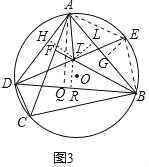
∵![]() =
=![]()
∴∠EAB=∠EDB=∠EDA,AE=BE,
∵∠TAE=∠EAB+∠TAB,∠ATE=∠EDA+∠DAT,
∴∠TAE=∠ATE,
∴AE=TE,
∵DT=TE,
∴AE=DT,
∵∠AGE=∠DHT=90°,
∴△EAG≌△TDH(AAS),
∴AG=DH,
∵AE=EB,EG⊥AB,
∴AG=BG,
∴2DH=AB,
∵Rt△TDR≌Rt△TDH(HL),
∴DH=DR,同理可得AL=AH,BR=BL,
设DH=x,则AB=2x,
∵AD=8,DB=12,
∴AL=AH=8﹣x,BR=12﹣x,AB=2x=8﹣x+12﹣x,
∴x=5,
∴DH=5,AB=10,
设TR=TL=TH=h,DT=m,
∵S△ADB=![]() BDAQ=
BDAQ=![]() ADh+
ADh+![]() ABh+
ABh+![]() DBh,
DBh,
∴12AQ=(8+12+10)h,
∴AQ=![]() h,
h,
∵sin∠BDE=sin∠ADE,可得![]() =
=![]() =
=![]() ,
,
sin∠AED=sin∠ABD,可得![]() =
=![]() =
=![]() =
=![]() ,
,
∴![]() =
= ,
,
解得m=4![]() 或﹣4
或﹣4![]() (舍弃),
(舍弃),
∴DE=2m=8![]() .
.

 阅读快车系列答案
阅读快车系列答案【题目】甲、乙人5场10次投篮命中次数如图
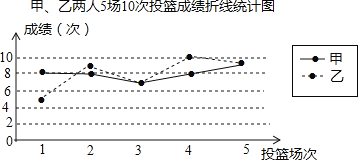
(1)填写表格.
平均数 | 众数 | 中位数 | 方差 | |
甲 | ______ | 8 | 8 | ______ |
乙 | 8 | ______ | ______ | 3.2 |
(2)①教练根据这5个成绩,选择甲参加投篮比赛,理由是什么?
②如果乙再投篮1场,命中8次,那么乙的投监成绩的方差将会怎样变化?(“变大”“变小”或”不变”)