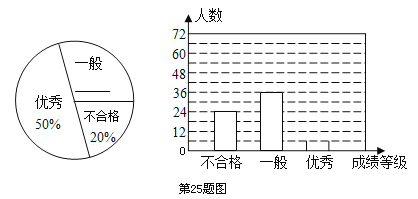
题目内容
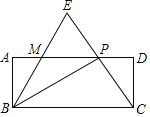
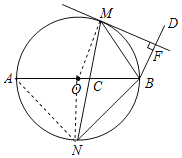
【题目】如图,M,N是以AB为直径的⊙O上的点,且![]() =
=![]() ,弦MN交AB于点C,BM平分∠ABD,MF⊥BD于点F.
,弦MN交AB于点C,BM平分∠ABD,MF⊥BD于点F.
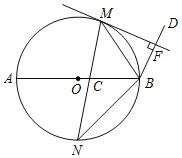
(1)求证:MF是⊙O的切线;
(2)若CN=3,BN=4,求CM的长.
【答案】(1)见解析;(2)CM=![]() .
.
【解析】
(1)根据等腰三角形的性质和角平分线的定义证得∠OMB=∠MBF,得出OM∥BF,即可证得OM⊥MF,即可证得结论;
(2)由勾股定理可求AB的长,可得AO,BO,ON的长,由勾股定理可求CO的长,通过证明△ACN∽△MCB,可得![]() ,即可求CM的长.
,即可求CM的长.
(1)连接OM,
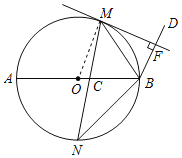
∵OM=OB,
∴∠OMB=∠OBM,
∵BM平分∠ABD,
∴∠OBM=∠MBF,
∴∠OMB=∠MBF,
∴OM∥BF,
∵MF⊥BD,
∴OM⊥MF,即∠OMF=90°,
∴MF是⊙O的切线;
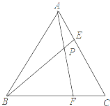
(2)如图,连接![]() ,
,![]()
![]()
![]() ,
,
![]()
![]() 是直径,
是直径,![]() ,
,
![]() ,
,![]()
![]()
![]()
![]()
![]() ,
,![]()
![]() ,
,![]()
![]()
![]()
![]()
![]()
![]()
![]()

练习册系列答案
相关题目