题目内容
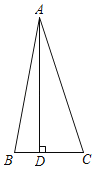
【题目】如图,点![]() 是等边
是等边![]() 内一点,且
内一点,且![]() ,点
,点![]() 是边
是边![]() 的中点,连接
的中点,连接![]() ,
,![]() .
.
(1)如图1,若点![]() ,
,![]() ,
,![]() 三点共线,则
三点共线,则![]() 与
与![]() 的数量关系是______;
的数量关系是______;
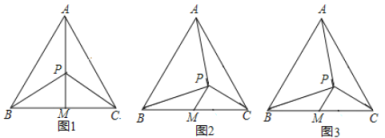
(2)如图2,若点![]() ,
,![]() ,
,![]() 三点不共线,问(1)中的结论还成立吗?若成立,请给出证明,若不成立,请说明理由;
三点不共线,问(1)中的结论还成立吗?若成立,请给出证明,若不成立,请说明理由;
(3)如图3,若![]() ,
,![]() ,直接写出
,直接写出![]() 的长是______.
的长是______.
【答案】(1)![]() ;(2)上述结论仍然成立,证明见解析;(3)
;(2)上述结论仍然成立,证明见解析;(3)![]()
【解析】
(1)由等边三角形的性质和已知条件得出∠BAC=∠ABC=∠ACB=60°,AM⊥BC,∠BAP=∠CAP=![]() ∠BAC=30°,得出PB=PC,由等腰三角形的性质得出∠PBC=∠PCB=30°,得出PC=2PM,证出∠ACP=60°-30°=30°=∠CAP,得出AP=PC,即可得出AP=2PM;(2)延长BP至D,使PD=PC,连接AD、CD,证明△ACD≌△BCP(SAS),得出AD=BP,∠ADC=∠BPC=120°,证明△CMN≌△BMP(SAS),得出CN=BP=AD,∠NCM=∠PBM,证明△ADP≌△NCP(SAS),即可得出AP=PN=2CM;(3)作CE⊥BD于E,设BP=4x,则PD=PC=3x,由等边三角形的性质得出PE=
∠BAC=30°,得出PB=PC,由等腰三角形的性质得出∠PBC=∠PCB=30°,得出PC=2PM,证出∠ACP=60°-30°=30°=∠CAP,得出AP=PC,即可得出AP=2PM;(2)延长BP至D,使PD=PC,连接AD、CD,证明△ACD≌△BCP(SAS),得出AD=BP,∠ADC=∠BPC=120°,证明△CMN≌△BMP(SAS),得出CN=BP=AD,∠NCM=∠PBM,证明△ADP≌△NCP(SAS),即可得出AP=PN=2CM;(3)作CE⊥BD于E,设BP=4x,则PD=PC=3x,由等边三角形的性质得出PE=![]() PD=
PD=![]() x,CE=
x,CE=![]() PE=
PE=![]() x,得出BE=BP+PE=
x,得出BE=BP+PE=![]() x,在Rt△BCE中,由勾股定理得出方程,求出x=2,得出AD=BP=8,PD=PC=6,作PF⊥AD于F,则∠DPF=30°,由直角三角形的性质得出DF=
x,在Rt△BCE中,由勾股定理得出方程,求出x=2,得出AD=BP=8,PD=PC=6,作PF⊥AD于F,则∠DPF=30°,由直角三角形的性质得出DF=![]() PD=3,PF=
PD=3,PF=![]() DF=3
DF=3![]() ,得出AF=AD-DF=8-3=5,由勾股定理即可得出答案.
,得出AF=AD-DF=8-3=5,由勾股定理即可得出答案.
(1)AP=2PM,理由如下:
∵△ABC是等边三角形,点M是边BC的中点,
∴∠BAC=∠ABC=∠ACB=60°,AM⊥BC,∠BAP=∠CAP=![]() ∠BAC=30°,
∠BAC=30°,
∴PB=PC,
∵∠BPC=120°,
∴∠PBC=∠PCB=30°,
∴PC=2PM,∠ACP=60°-30°=30°=∠CAP,
∴AP=PC,
∴AP=2PM;
故答案为:AP=2PM;
(2)AP=2PM成立,理由如下:
如图,延长BP至D,使PD=PC,连接AD、CD,
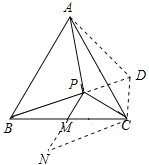
则∠CPD=180°-∠BPC=60°,
∴△PCD是等边三角形,
∴CD=PD=PC,∠PDC=∠PCD=60°,
∵△ABC是等边三角形,
∴BC=AC,∠ACB=60°=∠PCD,
∴∠BCP=∠ACD,
又∵AC=CB,
∴△ACD≌△BCP(SAS),
∴AD=BP,∠ADC=∠BPC=120°,
∴∠ADP=120°-60°=60°,
延长PM至N,使MN=MP,连接CN,
∵点M是边BC的中点,
∴CM=BM,
又∵∠CMN=∠PMB,
∴△CMN≌△BMP(SAS),
∴CN=BP=AD,∠NCM=∠PBM,
∴CN∥BP,
∴∠NCP+∠BPC=180°,
∴∠NCP=60°=∠ADP,
在△ADP和△NCP中,
 ,
,
∴△ADP≌△NCP(SAS),
∴AP=PN=2CM;
(3)如图,延长BP至D,使PD=PC,连接AD、CD,延长PM至N,使MN=MP,连接CN,作CE⊥BD于E,

同(2)得:AD=BP,AP=2CM;
设BP=4x,则PD=PC=3x,
∵CE⊥BD,△CPD是等边三角形,
∴PE=![]() PD=
PD=![]() x,CE=
x,CE=![]() PE=
PE=![]() x,
x,
∴BE=BP+PE=![]() x,
x,
∵△ABC是等边三角形,
∴BC=AB= ![]() ,
,
在Rt△BCE中,由勾股定理得:
解得:x=2,
∴AD=BP=8,PD=PC=6,
作PF⊥AD于F,则∠DPF=90°-60°=30°,
∴DF= ![]() PD=3,PF=
PD=3,PF= ![]() DF=3
DF=3 ![]() ,
,
∴AF=AD-DF=8-3=5,
∴![]() ;
;
故答案为:![]() .
.

 学业测评一课一测系列答案
学业测评一课一测系列答案【题目】今年,号称“千湖之省”的湖北正遭受大旱,为提高学生环境意识,节约用水,某校数学教师编制了一道应用题:为了保护水资源,某市制定一套节水的管理措施,其中对居民生活用水收费作如下规定:
月用水量(吨) | 单价(元/吨) |
不大于10吨部分 | 1.5 |
大于10吨不大于m吨部分(20≤m≤50) | 2 |
大于m吨部分 | 3 |
(1)若某用户六月份用水量为18吨,求其应缴纳的水费;
(2)记该用户六月份用水量为![]() 吨,缴纳水费为
吨,缴纳水费为![]() 元,试列出
元,试列出![]() 与
与![]() 的函数式;
的函数式;
(3)若该用户六月份用水量为40吨,缴纳水费![]() 元的取值范围为
元的取值范围为![]() ,试求
,试求![]() 的取值范围.
的取值范围.
各位同学,请你也认真做一做,相信聪明的你一定会顺利完成.