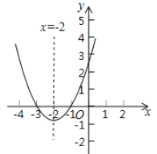题目内容
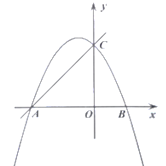
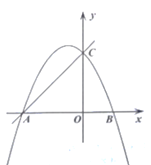
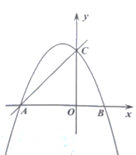
【题目】在平面直角坐标系xOy中,抛物线![]() 与y轴交于C点,与x轴交于A,B两点(点A在点B左侧),且点A的横坐标为-1.
与y轴交于C点,与x轴交于A,B两点(点A在点B左侧),且点A的横坐标为-1.

(1)求a的值;
(2)设抛物线的顶点P关于原点的对称点为![]() ,求点
,求点![]() 的坐标;
的坐标;
(3)将抛物线在A,B两点之间的部分(包括A, B两点),先向下平移3个单位,再向左平移m(![]() )个单位,平移后的图象记为图象G,若图象G与直线
)个单位,平移后的图象记为图象G,若图象G与直线![]() 无交点,求m的取值范围.
无交点,求m的取值范围.
【答案】a=-2;P′(-1,-4);m>![]()
【解析】
解:(1)∵A(﹣1,0)在抛物线![]() 上,
上,
∴![]() ,解得a = -2.
,解得a = -2.
(2)抛物线表达式为![]() .
.
∴顶点P的坐标为(1,4).
∵点P关于原点的对称点为P ′,
∴P ′的坐标为(-1,-4) .
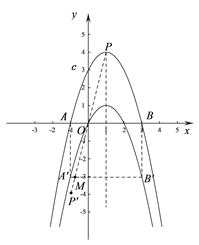
(3)易知直线PP ′的表达式为![]() ,
,
图象向下平移3个单位后,A ′的坐标为(-1,-3),
B′的坐标为(3,-3),设A ′B ′与PP ′的交点为点M,
若图象G与直线PP ′无交点,则B ′要左移到M及左边,
令y=-3代入直线PP ′的解析式,则![]() ,
,
M的坐标为![]() ,
,
∴B ′M=![]() ,
,
∴![]() .
.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目