��Ŀ����
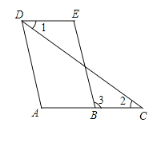
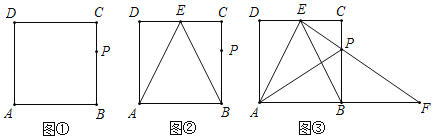
����Ŀ����ͼ���ھ���ABCD�У�AB�T2��AD=![]() ��P��BC���ϵ�һ�㣬��BP=2CP��
��P��BC���ϵ�һ�㣬��BP=2CP��
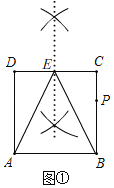
��1���ó߹���ͼ��������CD���ϵ��е�E������AE��BE��������ͼ�ۼ�����д��������
��2����ͼ�ڣ��ڣ�1���������£��ж�EB�Ƿ�ƽ�֡�AEC����˵�����ɣ�
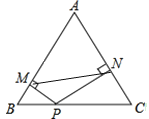
��3����ͼ�ۣ��ڣ�2���������£�����EP��͢����AB��͢�����ڵ�F������AP�������Ӹ����ߣ���PFB�ܷ��ɶ�����P������α任����PAE���һ�����������Σ�����ܣ�˵�����ɣ���д�����ַ�����ָ���Գ��ᡢ��ת���ġ���ת�����ƽ�ƾ��룩
���𰸡���1����ͼ����������2��EB��ƽ�֡�AEC�����ɼ������� ��3����PFB���ɶ�����P������α任���PAE���һ�����������Σ��任�ķ���Ϊ������BPF�Ƶ�B˳ʱ����ת120���͡�EPA�غϣ�����PF�۵�������AE�۵���
����������1���������߶εĴ�ֱƽ���ߵķ�����ͼ���ɵó����ۣ�
��2�������DE=CE=1�������жϳ���ADE�ա�BCE���ó���AED=��BEC������������Ǻ��������AED�����ɵó����ۣ�
��3�����жϳ���AEP�ա�FBP�����ɵó����ۣ�
��1������������ͼ����ͼ����ʾ��
��2��EB��ƽ�֡�AEC�����ɣ�
���ı���ABCD�Ǿ��Σ�
���C=��D=90�㣬CD=AB=2��BC=AD=![]() ��
��
�ߵ�E��CD���е㣬
��DE=CE=![]() CD=1��
CD=1��
����ADE����BCE�� ��
��
���ADE�ա�BCE��
���AED=��BEC��
��Rt��ADE��AD=![]() ��DE=1��
��DE=1��
��tan��AED=![]() =
=![]() ��
��
���AED=60�㣬
���BCE=��AED=60�㣬
���AEB=180�㩁��AED����BEC=60��=��BEC��
��BEƽ�֡�AEC��
��3����BP=2CP��BC=![]() =
=![]() ��
��
��CP=![]() ��BP=
��BP=![]() ��
��
��Rt��CEP��tan��CEP=![]() =
=![]() ��
��
���CEP=30�㣬
���BEP=30�㣬
���AEP=90�㣬
��CD��AB��
���F=��CEP=30�㣬
��Rt��ABP��tan��BAP=![]() =
=![]() ��
��
���PAB=30�㣬
���EAP=30��=��F=��PAB��
��CB��AF��
��AP=FP��
���AEP�ա�FBP��
���PFB���ɶ�����P������α任����PAE���һ�����������Σ�
�任�ķ���Ϊ������BPF�Ƶ�B˳ʱ����ת120������EPA�غϣ�����PF�۵�������AE�۵���

 ��У����ϵ�д�
��У����ϵ�д�