题目内容
【题目】如图是一道证明题,李老师已给同学们讲解了思路.请你将过程和理由补充完整.
已知∠1=∠2,∠A=∠E. 求证:AD∥BE.
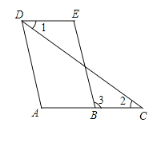
证明:∵∠1=∠2 (已知)
∴AC∥________(___________________________________)
∴∠3= _______ (___________________________________)
又∵∠A=∠E(___________)
∴∠A=______(___________________)
∴AD∥BE (_________________________________________)
【答案】DE 内错角相等,两直线平行 ∠E 两直线平行,内错角相等 已知 ∠3 等量代换 同位角相等,两直线平行
【解析】
根据内错角相等,两直线平行可得AC∥DE,然后根据两直线平行,内错角相等可得∠3=∠E,利用等量代换即可证出∠A=∠3,最后根据同位角相等,两直线平行即可证出结论.
证明:∵∠1=∠2 (已知)
∴AC∥DE(内错角相等,两直线平行)
∴∠3= ∠E(两直线平行,内错角相等)
又∵∠A=∠E(已知)
∴∠A=∠3(等量代换)
∴AD∥BE (同位角相等,两直线平行)
故答案为:DE;内错角相等,两直线平行;∠E;两直线平行,内错角相等;已知;∠3;等量代换;同位角相等,两直线平行.

练习册系列答案
相关题目